Team:SUSTech Shenzhen/Worms Locomotion Model

Worms Locomotion

Model

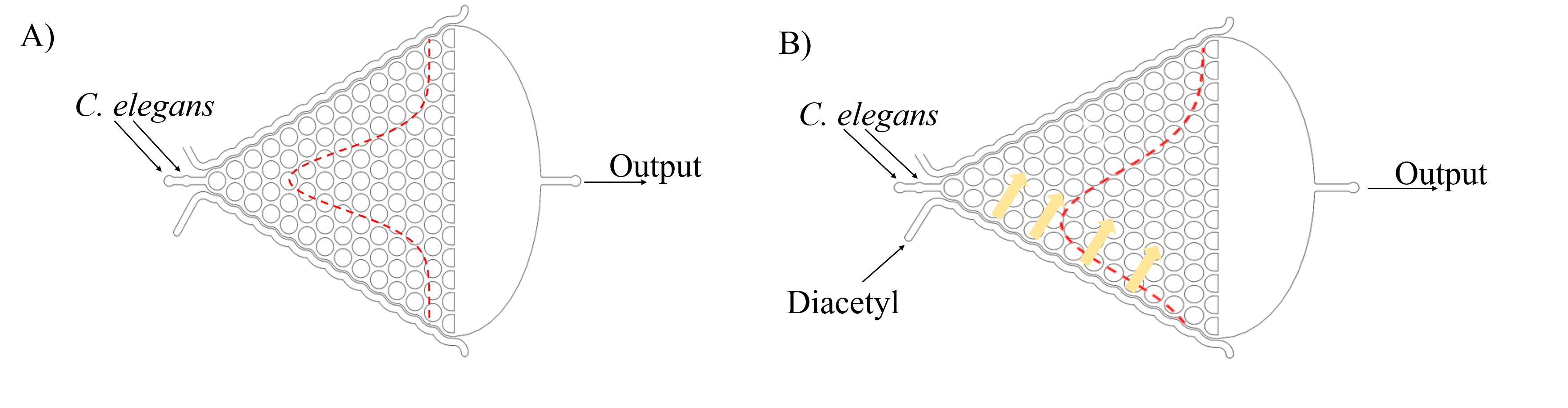
This model describes the locomotion of worms in the Gaussian Plate ( the second layer of the microfluidic chip). It is based on the mathematic model of the Galton Nail Plate (Figure 1.)

Different from classical Galton board(Fig.1), it is worms rather than balls running on the plate. We use worms as the “ball”. However, when a worm is choosing a direction at the crossing, its previous choice may influence current choice due to worm’s relative long body.

Fig. 1 The simulation of Galton board

This model is applied in the experiment to demonstrate whether the insertion undermine the function of AWA and AWB neurons. Worms with normal neurons will be attracted by diacetyl and be repelled by 2-nonanone.

Fig. 2 The Gaussian distribution A) The ideal Gaussian distribution before adding chemicals. B) The changed Gaussian distribution after adding chemicals by using the first diffusion methods, which means diacetyl diffuse in the same plate as the Gaussian Plate .

Building A Mathematic Model

Whether the Gaussian Plate works as our expectation is the main concern in this experiment. Different from classical Galton board, there are worms rather than balls running on the plate. The previous choice of them may affect the current choice due to their relatively long body.

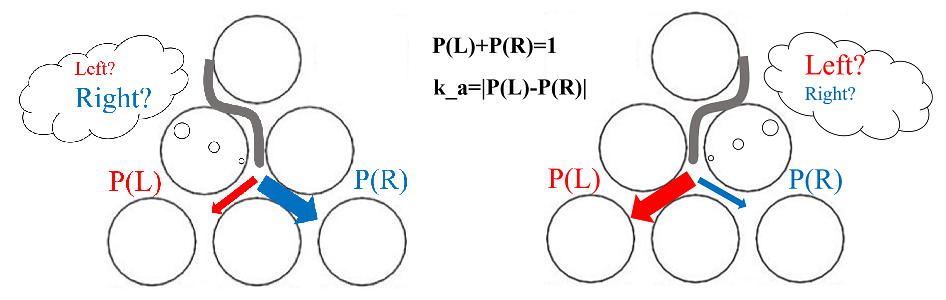
We introduced a parameter ‘k_a’ (0<=k_a<=1) in our model to describe the extent that the previous choice will influences on the current choice.

The ‘k_a’ is defined as the absolute value of difference between the probability of two direction choices (Fig 3. ).

Fig 3. Diagram of parameter ‘k_a’. ‘k_a’equals to absolute value of difference between the probability of two direction choices.

It means the greater the ‘k_a’ is the greater the influence of previous choice is. Especially, when ‘k_a’ is zero, the simulation model is more like Gaussian distribution.

We counted the number of C. elegans in each channel and calculated the parameter ‘k_a’ without chemical at first(Fig 4.).

Gaussian distribution is very common in nature and important in statistics. This distribution is tied to many natural phenomena. In our experiment, we use the Gaussian Plate to see C. elegans’’ distribution. Then we use it to see the change of C. elegans’’ distribution after adding attraction or repellent factor (Fig.2).

Firstly, we introduced a parameter ‘k_a’ (0<=k_a<=1) to describe how much the previous choice influences the current choice

The ‘k_a’ is defined as the absolute value of the difference between the probability of two direction choices.

Fig. 4 the Gaussian Plate to study locomotion on-chip

It means the greater the ‘k_a’ is the greater the influence of previous choice is. Especially, when ‘k_a’ is zero, the simulation model is more like Gaussian distribution.

We counted the number of C. elegans in each channel and calculated the parameter ‘k_a’ at first (Fig.4).

Count	Firstly Turn Left	Firstly Turn Right
Secondly Turn Left	28	9
Secondly Turn Right	12	14

k=\frac{same turning-different turning}{total turning}=\frac{(28+14-12-9)}{(28+14+12+9)}=0.3

Assume that ‘k_a’ doesn’t change when we add attraction or repellent factors. Then this model can be used to stimulate C. elegans preference considering ‘k_a’.

We can analyze how much the factor attracts or repels the C. elegans by introducing another parameter ‘k_perf’ (0<=k_perf<=1).

Both parameters set above are dependent on the assumption that parameters values are proportional to the probability they affect the C. elegans’ choice.

For example, if ‘k_a’ is to ‘0’, previous choice doesn’t affect current choice at all. If ‘’k_a is ‘1’, the worm’s next choice is totally determined by the previous choice and the final result will show polarized distribution( C. elegans only pass through the rightmost or leftmost channels). When ‘k_a’ is 0.5, a worm has 25% probability of turning right/left and 75% probability of turning left/right at a crossing. ‘k_b’ (attraction or repellent parameter) is the same as ‘k_a’

Comparing simulation results with experimental data

Simulation results are shown in two steps:

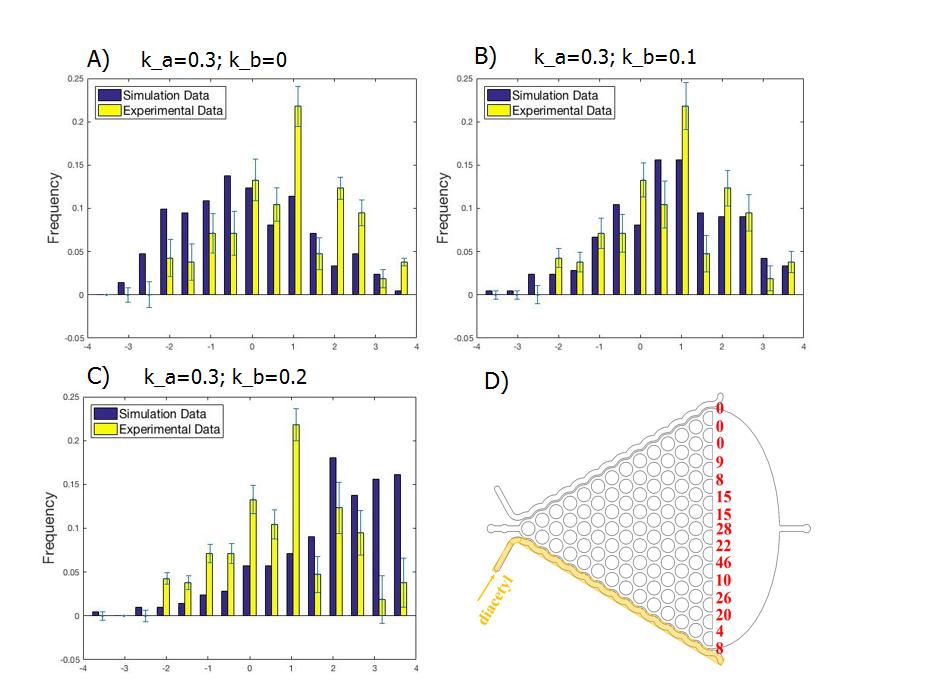
1. Determine parameter ‘k_a’: According to the observation above, ‘k_a’ = 0.3.
2. Compare the simulation result (10000 worms) with the experimental data (193 worms) without chemical added. Chi-square test is used to examine the goodness of fit (X2)

Figure 5. A) Compare the simulation data (10000 worms, k_a=0.3, purple bar) with Gaussian distribution ( blue line) B) Compare the experimental data( 193 wildtype worms, yellow bar) with the simulation data (10000 worms, k_a=0.3, purple bar). X2= 17.19 (degree of freedom is 14, p value is 0.95). C) Raw counts in experiment (193 wildtype worms, without adding chemical) D) An example of experimental images

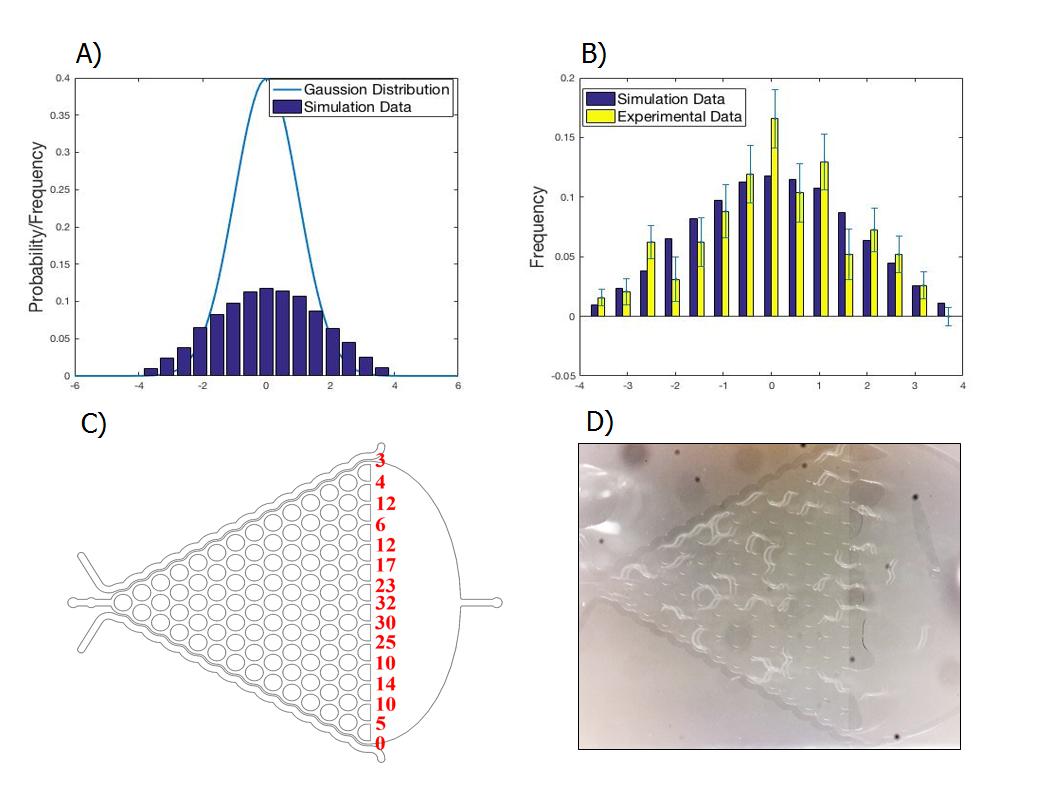
1. We simulate the process with the same number (193 worms) as the number of worms used in experiment.

Figure 6. A) Compare the simulation data (193 worms, k_a=0.3, purple bar) with Gaussian distribution ( blue line) B) Compare the experimental data ( 193 wild types, yellow bar) with the simulation data (193 worms, k_a=0.3, purple bar). X2= 20.11 (degree of freedom is 14, p value is 0.95).

1. Compare simulated data with experimental data after adding diacetyl by using different 'k_b'( parameter set for showing attraction or repellent to C. elegans ). k_b is about 0.1.

Figure 7. Fitting of model parameter on experiments with the addition of diacetyl. (a)Compare the experimental data (197 wildtype worms, yellow bar) with the simulation data (197 worms, k_a=0.3, k_b=0, purple bar). X2= 170.83 (degree of freedom is 14, p value is 0.995). (b)Compare the experimental data (197 wildtype worms, yellow bar) with the simulation data (197 worms, k_a=0.3, k_b=0.1, purple bar). X2= 39.62 (degree of freedom is 14, p value is 0.995). (c)Compare the experimental data (197 wildtype worms, yellow bar) with the simulation data (197 worms, k_a=0.3, k_b=0.2, purple bar). X2= 219.28 degree of freedom is 14, p value is 0.995). (d)Raw counts in experiment (197 wildtype worms, induced by diacetyl)

Conclusion

·In the experiment, the “influence factor” of previous choice-making k_a=0.3. It means that if a worm turn left at the first crossing, the possibility of turning left at the second crossing is will be 30% more than that of turning right.

·The “attraction factor” of diacetyle to worms k_b=0.1. The added diacetyl will attract worms toward the side with higher diacetyle concentration.

Made by from the elegans.Inc in SUSTech_Shenzhen.

Licensed under CC BY 4.0.

• ©2017 SUSTech_Shenzhen