| Line 1: | Line 1: | ||
{{Aix-Marseille|title=Modelling PLP production|toc=__NOTOC__}} | {{Aix-Marseille|title=Modelling PLP production|toc=__NOTOC__}} | ||
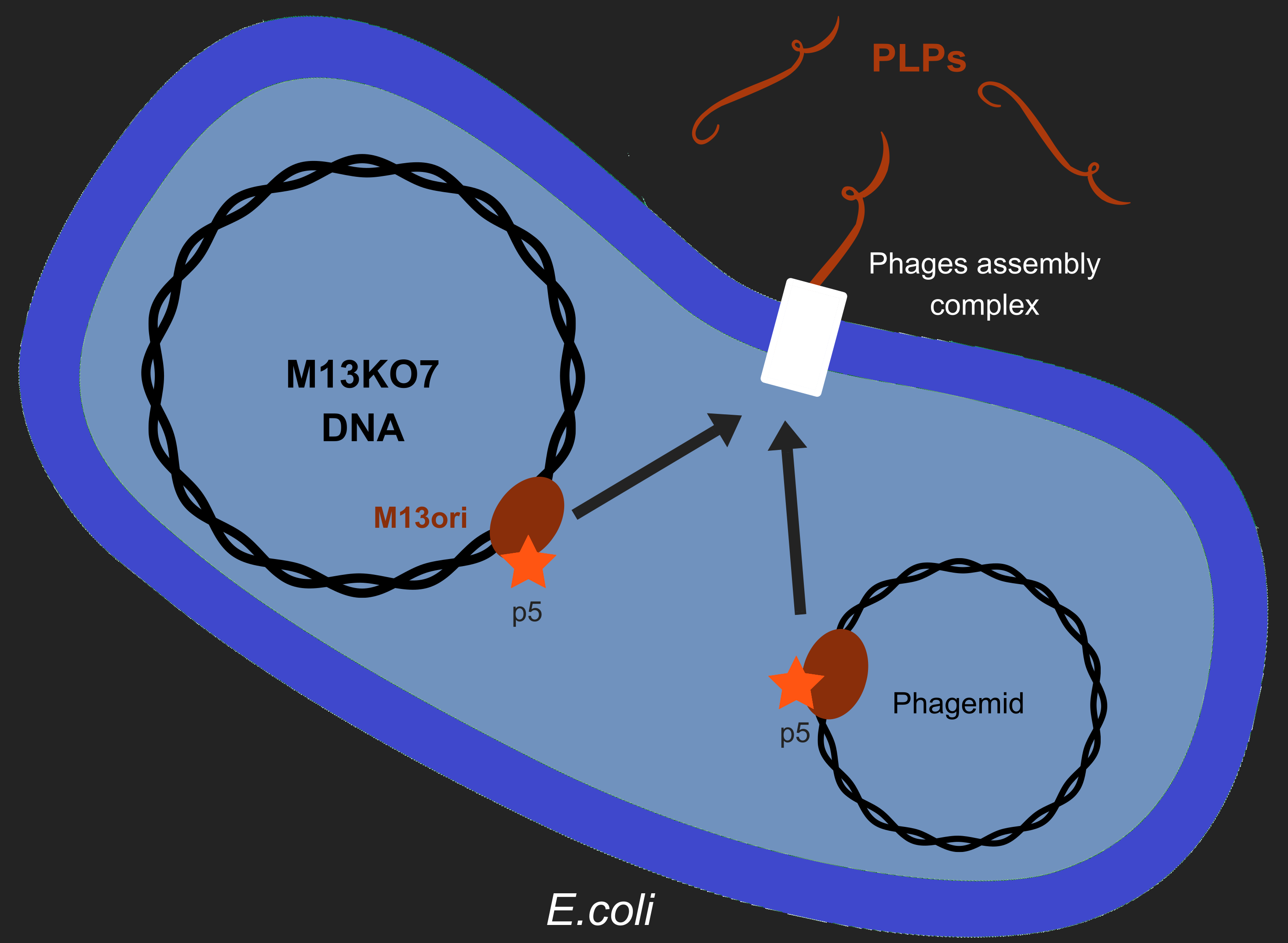
| − | [[File:T--Aix-Marseille--ModelM13.png|400px|right|thumb|Figure1: | + | [[File:T--Aix-Marseille--ModelM13.png|400px|right|thumb|Figure1: To produce PLPs, bacteria must contain both a helper phage (like M13KO7), that codes for the different phage proteins, and also a phagemid, that encodes the toxic gene we want to include in the PLP. |
If M13KO7 is packaged a replicative phage is produced, which we do not want, and if the phagemid it packaged then a PLP is produced.]] | If M13KO7 is packaged a replicative phage is produced, which we do not want, and if the phagemid it packaged then a PLP is produced.]] | ||
Revision as of 20:05, 1 November 2017
Modelling PLP production
The problem
Our objective is to produce phage like particles (PLP), for this, the bacteria must contain both a helper phage and also a phagemid (Figure 1). During phage production, several key events determine which DNA molecules are packaged into phage or PLP. These involve recognition of the M13 replication origin by several phage proteins.
A major hurdle to marketing KILL XYL is obtaining the necessary authorizations. Our interviews and legislation study both showed that the number of viable phages could be a problem. We therefore decided to measure and model the ratio between viable phage and phage-like particles, and so try to optimize this ratio to facilitate the preparation of pure PLP.
The Model
We based our model on a recently published model of "wild-type" M13 replication [1] [2].
This model was modified to accomodate the fact our system has two plasmids (Helper and Phagemid) when Smeal's has only one. This means we incorporated: the presence of a phagemid, with its own replicative origin and M13 origin, the helper-phage E. coli plasmid origin and the modification of the helper-phage M13 origin. This was done either through adapting pre-existing species, parameters and equations, or creating new ones. These modifications added 9 species and 3 parameters to the original model, and changed 5 other pre-existing species and 3 other pre-existing parameters. 13 new equations were created.
The modified model is available File:T--Aix-Marseille--Model.zip
We used the initial measurement to constrain parameters of the model, along with published numbers for the number of copies of plasmids with different replicative origins.
Results
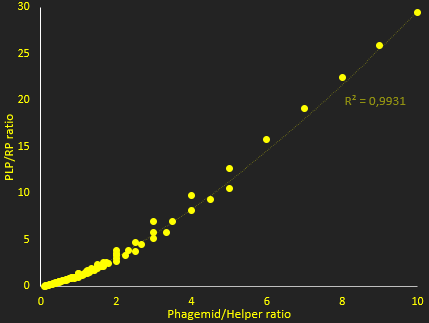
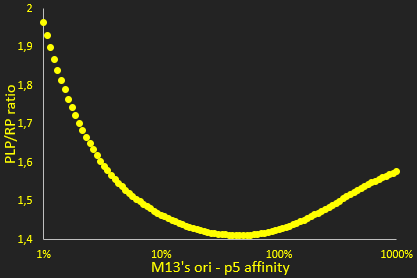
The packaging ratio depends on two main parameters: the initial ratio of transfected phagemid and helper phage (Figure 2), and the difference in p5 affinity for eitheir plasmid's M13 ori (Figure 3). We also observed increasing the number of transfected plasmids increased production, up to a certain point, which we determined (Figure 4).
According to our model, the optimal PLP-producing cell factory will have 6 transfected phagemids and 2 helper phages. This can be controled by adjusting the quantity of DNA added in the transfection chamber.
Conclusions
Clearly the initial design needs to be improved to increase the proportion of PLP produced.
The model has shown as that the parameters of prime importance for determining the proportion of PLP produced are .... .- ↑ Smeal et al, Simulation of the M13 life cycle I: Assembly of a genetically-structured deterministic chemical kinetic simulation, Virology, 500, January 2017
- ↑ Smeal et al, Simulation of the M13 life cycle II: Investigation of the control mechanisms of M13 infection and establishment of the carrier state, Virology, 500, January 2017