Figure1: To produce PLPs, bacteria must contain both a helper phage (like M13KO7), that codes for the different phage proteins, and also a phagemid, that encodes the toxic gene we want to include in the PLP. If M13KO7 is packaged a replicative phage is produced, which we do not want, and if the phagemid it packaged then a PLP is produced.

The problem

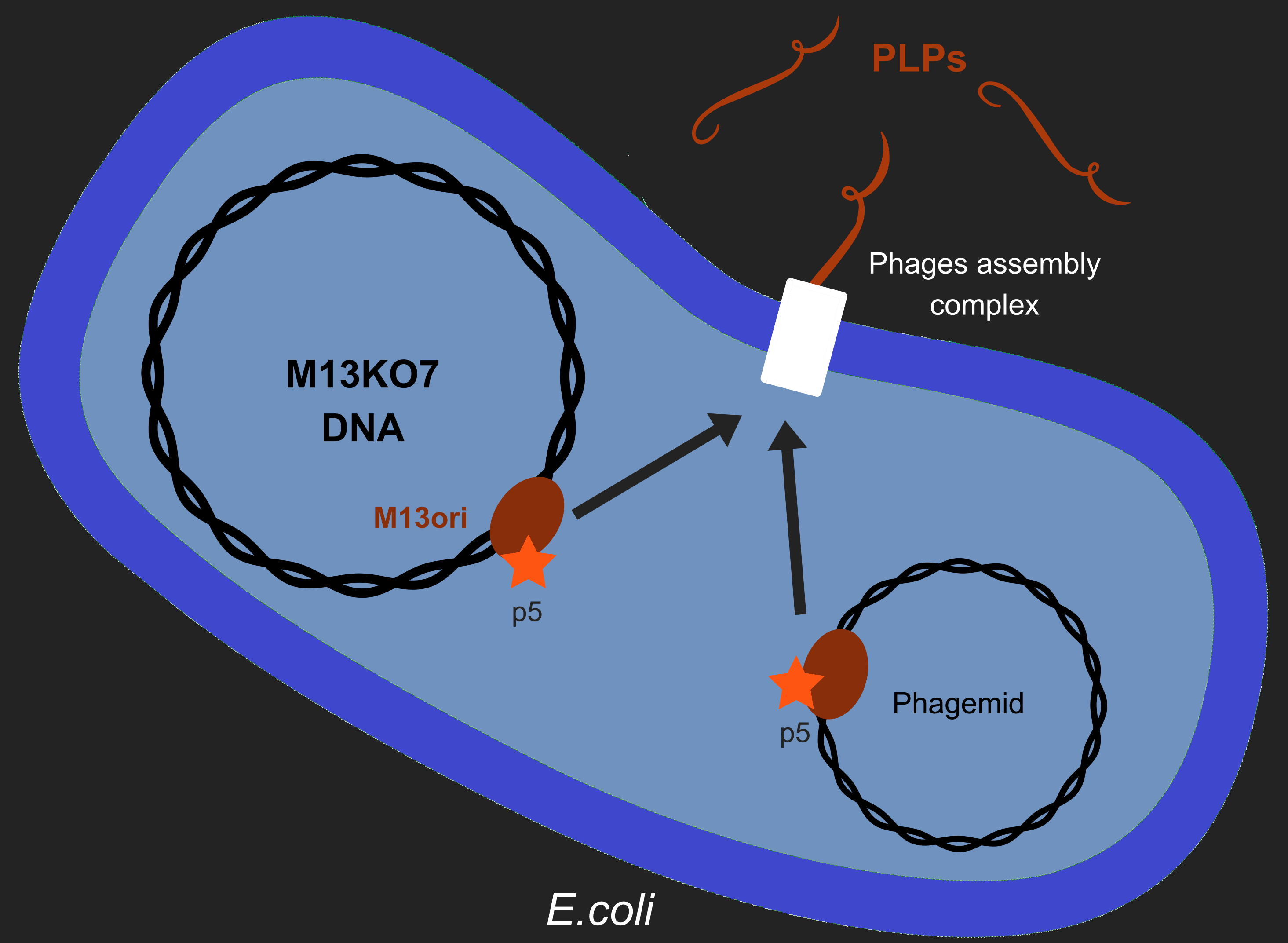
Our objective is to produce phage like particles (PLP), for this, the bacteria must contain both a helper phage and also a phagemid (Figure 1). During phage production, several key events determine which DNA molecules are packaged into phage or PLP. These involve recognition of the M13 replication origin by several phage proteins.

A major hurdle to marketing KILL XYL is obtaining the necessary authorizations. Our interviews and legislation study both showed that the number of viable phages could be a problem. We therefore decided to measure and model the ratio between viable phage and phage-like particles, and so try to optimize this ratio to facilitate the preparation of pure PLP.

The Model

We based our model on a recently published model of "wild-type" M13 replication ^{[1] [2]}.

This model was modified to accommodate the fact our system has two plasmids (Helper and Phagemid) while the previously modeled system has only one. This means we incorporated: the presence of a phagemid, with its own replicative origin and M13 origin, the helper-phage E. coli plasmid origin and the modification of the helper-phage M13 origin. This was done by adapting the existing model and adding new parts to the existing model. These modifications added 9 species and 3 parameters and 13 equations to the original model, and changed 8 parts of the previous model.

We observed we could roughly reproduce the published copy number of plasmids by tweaking our parameter describing the affinity of DNA polymerase for the plasmid's origin of replication ("Polymerase Binding Event") in our model when the reactions describing phage formation where inactivated. This is a purely empirical observation. To the best of our knowledge, their is no published data describing this parameter, which is why we assumed published data for plasmid copy number can be used as a proxy to approximate the proclivity of DNA polymerase to bind the plasmid's origin of replication.

The modified model is available File:T--Aix-Marseille--Model.zip

We used the initial measurement to constrain parameters of the model.

Results

Figure2: Scan for the optimal initial ratio of transformed helper phage and phagemid. Simulation of the PLP/RP ratio as a function of the helper phage and phagemid ratio (100 data points). The trend line represents a power law. We simulated our model over a time course of 24h.

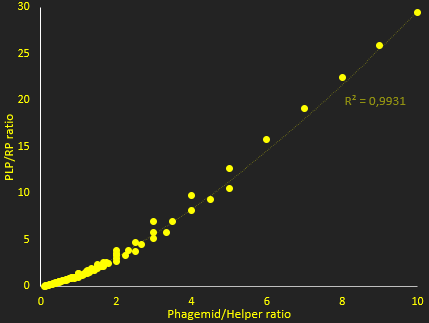
The packaging ratio depends on two main parameters: the initial ratio of transformed phagemid and helper phage (Figure 2), and the difference in p5 affinity for eitheir plasmid's M13 ori (Figure 3).

In figure 2, we investigate how the ratio of PLP to replicative phage depends on the copy number of the two plasmids used. This shows that higher copy numbers of phagemid increase this ratio. This simulation showed essentially that increasing copy number increases packaging efficiency, and ratio of PLP to phage. The resut hide however, that at very high ratios, the lack of protein reduces production. Nevertheless, and in view of this result for the tests we used a backbone that gives, in theory, a very high copy number for the phagemid, to try and maximize the ratio of PLP to phage.

Figure3: Scan to find the M13 origin-P5 affinity that optimizes production of phage-like particles. This parameters is reduced by the engineering of the M13 origin of replication in helper phage. Helper phage affinity for p5 is expressed as a fraction of the wild-type original affinity. We simulated our model over a time course of 24h.

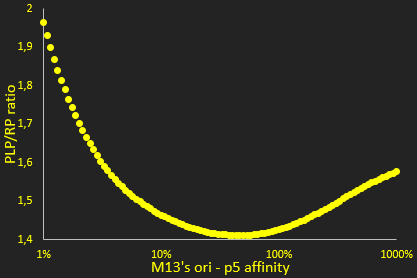
The next parameter we investigated was the relative affinity of the phagemid and helper phage origins of replication for the p5 protein (Figure 3). This affinity is critical in the model for determining wether single stranded DNA is used for packaging or making additional double stranded DNA.

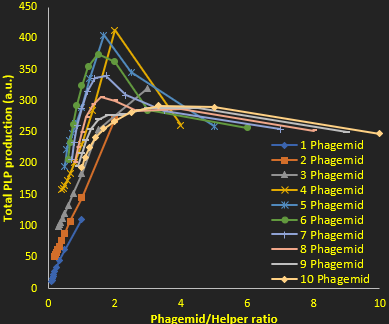
As we mentioned previously in figure 2, the higher the phagemid to helper ratio the better the PLP to replicative phage ratio in the end. Yet this better purity is offset by a drop in the quantity of PLPs produced, due to a lack of proteins (which are encoded by the helper phage). This is why we also plotted the total PLP production against phagemid to helper ratio (Figure 4). This allowed us to determine the optimal conditions for maximal production of PLPs at a decent quality: having a copy number around 10 phagemids and 2 helpers per cell. This allows both decent PLP production while ensuring very high purity of the produced particles.

Figure4: Total PLP production for an array of Phagemid and Helper initial conditions. We simulated our model over a time course of 24h. Initial number of Helper and Phagemid varied from 1 to 10.

Conclusions

Clearly, our measurements show the initial design needs to be improved to increase the proportion of PLP produced. The model has shown that the parameters of prime importance for determining the proportion of PLP produced are plasmid copy number and affinity between the M13 ori and protein p5, as we have shown in figures 2 through 4.

So to implement our project it will be necessary to redesign certain features. Specifically, we should

1. ↑ Smeal et al, Simulation of the M13 life cycle I: Assembly of a genetically-structured deterministic chemical kinetic simulation, Virology, 500, January 2017
2. ↑ Smeal et al, Simulation of the M13 life cycle II: Investigation of the control mechanisms of M13 infection and establishment of the carrier state, Virology, 500, January 2017