Gas Vesicle Structure
Gas vesicles are proteineceous nano-structures that are utilized by many aquatic micro-organisms like halo-bacteria and some algae to provide buoyancy. The structure and arrangement is highly conserved between organisms with width being almost the only widely varying parameter. They contain gases which diffuse in during formation and are kept localised by the hydrophobicity of the inner membrane.
Unlike true vesicles, these are made of proteins instead of phospholipids and are hence of considerable interest. Each gas vesicle is composed of two primary protein monomers, the gas vesicle forming proteins A (GvpA) and C (GvpC). The entire structure will be discussed in the following sections.
Electron micrograph of gas vesicles isolated from A. flos-aquae (left) and H. Salinarium (right). Taken from [1].
The easiest way to assay presence of gas vesicles is their disappearance under high pressure under a microscope. This was observed even during normal experiments. Fully filled micro-centrifuge tubes containing dilute gas vesicle suspensions lost their faint opalescence when the tube was closed (this did lead to a loss of samples). A more strict assay was done using DLS (See Dynamic Light Scattering) and SEM Imaging to pinpoint the exact size of the nano-particles. It was found that these gas vesicles have an effective hydrodynamic radius of around 230nm. This estimate was particularly valuable in the development of our model.
GvpA
The gas vesicle forming protein A (~8kDa) forms the main ribbed structure of the gas vesicle. The 3-Dimensional structural model of the protein was recently analysed by Strunk et al[2]. As was noted, the best probable docking pattern in a vesicle involves formation of a dimer and their consequent stacking. We intended to re-create the whole gas vesicle structure from this data and try to explain the growth pattern noticed during their formation. It is interesting to note that the hydrophobicity of the internally exposed part of GvpA is what keeps the gases from diffusing out.

3D folded structure of gas vesicle forming protein A (Adapted from [2])
GvpC
The gas vesicle forming protein C is the second most abundant protein found in the nanostructure. It is still far rarer compared to GvpA (1:25 molar ratio[3]) and does not contribute to the structure but rather to the integrity of the gas vesicle. The vesicles used in the various experiments were stripped of GvpC before use and hence were much more sensitive compared to wild type gas vesicles. The critical pressure for the gas vesicles was found to reduce drastically on the removal of this protein.
Stacking of proteins in a GV nanoparticle
3-Dimensional structure of the nanoparticle
Effective buoyant density
Most of the physical properties of the gas vesicles were uncovered by Walsby et al. in their 1994 review[4] . They calculated the average buoyant density of a gas vesicle to be around 120kgm-3. Note that while this density if much less than that of water, it doesn’t necessarily imply a flotation advantage due to the presence of diffusive forces in a suspension. The smaller the particle, higher is the magnitude of these diffusive interactions and more is the deviation from the ideal concentration profile in a column. The mathematical model part of our project deals with finding how these profiles evolve for overtime and how this evolution changes when we purposefully make them flocculate using agents like chitosan and biotin-streptavidin.
Mathematical Model
The following sections detail the development of our model which deals with the dynamics of gas vesicle motion in a medium and how their concentration profiles change over time.
Terminal Velocity
A floating particle in a media experiences multiple types of forces, some of which are more prominent than others. Given the buoyant density of the particle, we can find the terminal velocity by equating all the upward forces to the downward ones and solving for velocity from the stokes’ drag term.

Assuming the gas vesicle to be of the shape given above, its volume in terms of length l, half angle θ and radius r is given by,
\[ V = \pi r^{2}(l+\frac{2}{3}r cot \theta) \tag{1.1} \label{eq:1.1} \]So, the buoyant force on the gas vesicle is given by,
\[ F_b=V\rho g = \rho g\pi r^{2}(l+\frac{2}{3}r cot \theta) \tag{1.2} \label{eq:1.2} \]Where ρ is the density of the media.
Similarly, the force due to gravity is,
\[ F_w=V\rho_{gv} g = \rho_{gv} g\pi r^{2}(l+\frac{2}{3}r cot \theta) \tag{1.3} \label{eq:1.3} \]Where ρgv is the buoyant density of the gas vesicle.
When the particle reaches its terminal velocity, all the forces are balanced. Thus we can equate,
\[ F_{d} + F_{w} = F_{b} \tag{1.4} \label{eq:1.4} \]The viscous drag is usually a complex function of particle shape and size, in our case however, the DLS experiment directly gives the hydrodynamic radius of the particle. Hence we can use the well known expression for drag on a spherical particle given by,
\[ F_{d}=6\pi\eta R_{H} v \tag{1.5} \label{eq:1.5} \]Where vt is the terminal velocity and RH the hydrodynamic radius.
Solving for vt, we get
\[ v_{t}=\frac{Vg}{6\pi\eta R_H} (\rho-\rho_{gv}) \tag{1.6} \label{eq:1.6} \]The various parameters can be modified to find the terminal velocity for a particular kind of nanoparticle after measuring the hydrodynamic size with a DLS system. It is interesting to note that while the hydrodynamic radius is a linear function of the size of the gas vesicle, the volume scales as a cube of the radius. This leads to the logical deduction that the terminal velocity will increase if the particles are allowed to aggregate.
For a normal H. Salinarium gas vesicle, the terminal velocity comes out to be of the order of 10 nm/s . This is incredibly slow considering the size of a gas vesicle is an order of magnitude larger than this number.
Péclet number
The Péclet number is a dimensionless quantity that is used to determine the relative magnitudes of advective and diffusive transport phenomena. In the case of a particle undergoing flotation(or sedimentation), it can be easily calculated by taking the following ratio,
\[ P_e=\frac{Lu}{D} \tag{2.1} \label{eq:2.1} \]Where L is the characteristic length scale in the system (~200nm in the case of a gas vesicle), u the local velocity of the fluid and D the mass diffusion coefficient.
The Einstein relation for a spherical particle gives the Diffusion coefficient from the viscosity of the medium through the following relation,
\[ D=\frac{k_{b}T}{6\pi \eta R_{H}} \tag{2.2} \label{eq:2.2} \]Now, the terminal flow velocity from the last section can be used to calculate the Péclet number for this system. If the Péclet number is extremely small compared to 1, diffusion is dominant over advective transfer and must be considered during our calculations.
For a typical gas vesicle particle at room temperature (T = 273K),
L ~ 500nm
u ~ 10nm/s
RH ~ 200nm
Substituting these numbers in equation 2.2, we get a péclet number of the order of 10-3, which implies dominant diffusive effects when gas vesicles are allowed to settle at the equilibrium concentration profile. In such a case, a model is needed that can account for the behaviour of floating particles in the highly diffusive regime.
Evolution of gas vesicle concentration profile in a column
The first step to solving any problem relating to diffusive transport is writing a convection-diffusion equation that takes all intricacies of the underlying system into account. For a system of sedimenting particles, it is given by[5],
\[ \frac{\partial C}{\partial t}=\frac{\partial}{\partial h}(\frac{D \partial C}{\partial h})-\frac{\partial (C U(C))}{\partial h} \tag{3.1} \label{eq:3.1} \]Where U(C) is the settling velocity of a particle in a region where the concentration is C. The fact that this velocity is related to diffusion arises due to long range (compared to particle size) velocity field interactions in the column. Two particles settling together tend to sediment faster compared to a single one due to the presence of fluid flow around the seond one due to the motion of the first particle. If the suspension is sufficiently dilute and the particle sizes sufficiently small, these velocity fields can be ignored and each particle can be assumed to settle with a constant velocity (the terminal velocity). U(C) now reduces to -Vs, the terminal settling velocity (which is negative in this case because the particles are floating upwards).
The translational diffusion coefficient is not a height dependent parameter and can be taken out of the partial differential term giving the following equation in absence of an underlying velocity field,
\[ \frac{\partial C}{\partial t}=D \frac{\partial ^{2} C}{\partial h^{2}}+V_{s} \frac{\partial C}{\partial h} \tag{3.2} \label{eq:3.2} \]This equation can be solved either analytically or numerically to yield solutions as follows.
Analytical solution
A analytical solution easily follows on assuming solutions of the variable seperable form (note that this limits the form of initial distributions we can start with)
\[ C(h,t)=H(h)T(t) \tag{3.3} \label{eq:3.3} \]On appropriate rearrangement, we get
\[ \frac{1}{T(t)}\frac{\partial T(t)}{\partial t}=\frac{D}{H(h)}\frac{\partial^2 H(h)}{\partial h^2}+\frac{V_s}{H(h)}\frac{\partial H}{\partial h} \tag{3.4} \label{eq:3.4} \]The two sides of the equation being dependent on independent variables can be equated to a constant (say k). Integrating the left side of the equation with this constant, we get the time dependent part of the form,
\[ T(t)= T_{0} e^{k(t-t_0)} \tag{3.5} \label{eq:3.5} \]Where \(T_0\) is the value of T at \(t=t_0\).
The height dependent part when equated to \(k\) gives a homogeneous second order linear differential equation of the form \(ay"+by'+cy=0\) which has the general solution \(H(h)=C_1 e^{rh}+C_2 h e^{rh}\) (repeated roots, unique solution) where \(r=\frac{-b}{2a}\). Using this solution, the height dependent part of the concentration function comes out to be,
Also, the condition for repeated roots fixes the value of k (\(\frac{-V_s^2}{4D}\)). The final analytical solution of the above convection-diffusion equation comes out to be,
\[ C(h,t)=H(h)T(t)=T_0(C_1 e^{\frac{-V_s h}{D}}+C_2 h e^{\frac{-V_s h}{D}}) e^{\frac{-V_s^2}{4D} (t-t_0)} \tag{3.7} \label{eq:3.7} \]The immediate need now is to normalise the height dependent part of the equation to allow us to make reasonable predictions. \(T_0\) can be safely neglected allowing only \(C_1\) and \(C_2\) to take values that normalise the function.
Experimental Data
Visual Analysis
Flotation Spectrophotometry
Chitosan
Double replicates of four different concentrations of chitosan were used with gas vesicles (30ul stock) and the resulting solutions were diluted to 2ml to perform a flotation spectrophotometry assay.
| Tube Label | Effective gas vesicle concentration (ng/μl) |
Effective chitosan concentration (ng/μl) |
Remarks |
|---|---|---|---|
| 1 | 15 | 0 | Control tube |
| 2A | 15 | 5 | First replicate |
| 2B | 15 | 5 | Second replicate |
| 3A | 15 | 50 | First replicate |
| 3B | 15 | 50 | Second replicate |
| 4A | 15 | 500 | First replicate |
| 4B | 15 | 500 | Second replicate |
| 5A | 15 | 5000 | First replicate |
| 5B | 15 | 5000 | Second replicate |
The data from the spectrophotometer assays for chitosan can be found here.
An analysis of the data is given in the results section
Electron microscopy
Multiple dilutions of pure gas vesicles suspended in PBS were imaged under a Scanning Electron Microscope after applying a 10nm gold sputter. In the images, gas vesicles can be seen as translucent polygon shaped particles. Note that some lysed gas vesicle membranes are also seen in the image owing to the drying step during the sample preparation that precedes electron microscopy. Air drying can be carried out over a longer period of time to reduce the number of such events. Three dilutions were prepared for microscopy, out of these the 0.01ug/ul samples gave the best results.


Images 1 and 2: Gas vesicles at 40000x magnification under a SEM (0.01 ug/ul).
Dynamic Light Scattering
Gas vesicle suspensions prepared as in the spectrophotometry assay were used to perform Dynamic light scattering. Three replicates of each concentration were run through the machine thrice. It was noted that the average particle size decreased after every run indicating the particles were either sedimenting or floating up.
The data can be accessed here.
The theory behind dynamic light scattering becomes quite simple if the implications of Einstein's brownian motion hypothesis are well known. Smaller particles tend to get a stronger "kick" when a solvent particle hits them. What the system actually detects are the correlations that persist in the scattered intensities at consequent time intervals. A large correlation implies that the particle hasn't moved much in the interval and hence is larger.
The actual values obtained from the system are those of the translation diffusion coefficient, to which the software applies the famous Einstein relation (see Mathematical model) giving the hydrodynamic diameter, \[ d_{H}=\frac{kT}{3 \pi \eta D} \]where dH is the hydrodynamic diameter and D the translation diffusion coefficient.
Results
Chitosan
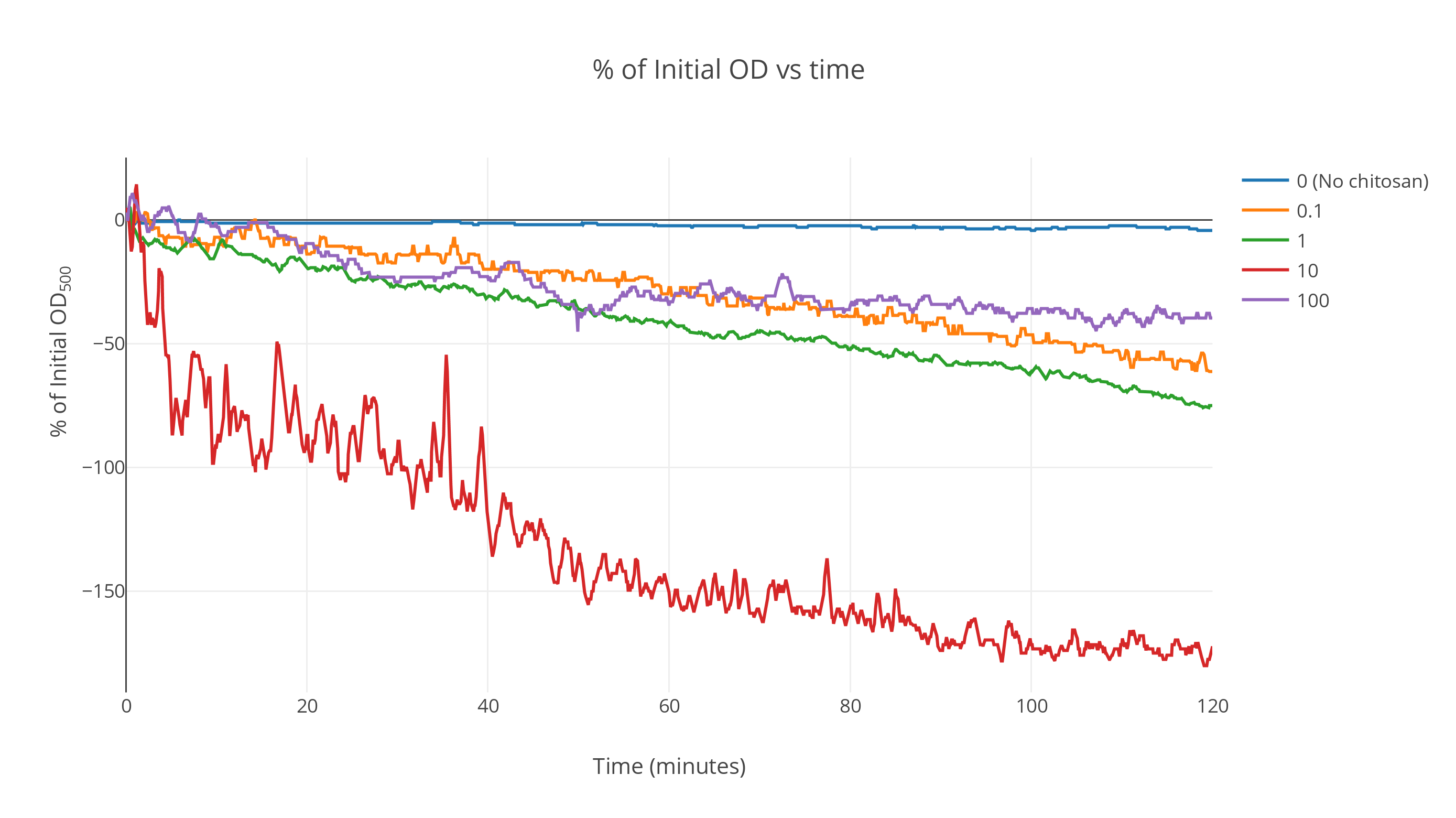
The data when averaged over the replicates shows a marked faster decrease in OD as time passes for chitosan treated gas vesicles. The gas vesicles without chitosan show no significant decrease over a duration of two hours while the ones with an intermediate chitosan concentration show a fast decrease at the start which saturates as time passes. All other curves lie above this one (Fig 1). At very high concentrations, it was seen that the saturation point shifted upwards. We postulate this is because of the gas vesicles being irreversibly denatured by the action of excessive acetic acid concentration during chitosan incubation. More detailed analysis can be conducted to find the optimum concentration at which maximum flotation is achieved. From these results, we expect it to be around the 500ng/ul order of magnitude.
The plot was smoothed out over a window of 85 data points giving the smooth profiles. (Fig 2)

It was found that the particle size increased considerably on addition of chitosan. The data from the Dynamic light scattering experiment is plotted in Figure 3. The points were fit to a quadratic curve.

References
[1] Daviso E, Belenky M, Griffin RG, Herzfeld J. Gas vesicles across kingdoms: a comparative solid state NMR study. Journal of molecular microbiology and biotechnology. 2013;23(0):10.1159/000351340. doi:10.1159/000351340.[2] Strunk, T., Hamacher, K., Hoffgaard, F., Engelhardt, H., Zillig, M. D., Faist, K., Wenzel, W. and Pfeifer, F. (2011), Structural model of the gas vesicle protein GvpA and analysis of GvpA mutants in vivo. Molecular Microbiology, 81: 56–68. doi:10.1111/j.1365-2958.2011.07669.x
[3] Buchholz B, Hayes P, Walsby A. Microbiology 139(10):2353-2363 doi:10.1099/00221287-139-10-2353
[4] Walsby AE. Gas vesicles. Microbiological Reviews. 1994;58(1):94-144
[5] Nielsen, Peter. Combined Convection-diffusion modelling of sediment entrainment. Coastal Engineering 1992 . doi:10.1061/9780872629332.244











