JackSuitor (Talk | contribs) |
JackSuitor (Talk | contribs) |
||
| Line 281: | Line 281: | ||
</figure><br><br><br><br> | </figure><br><br><br><br> | ||
| − | <p> We can see that under the default state, the pulse generator completes all the | + | <p> We can see that under the default state, the pulse generator completes all the steps within 2.5 hours. Although |
the pulse pattern can be seen, the magnitude and duration of each pulse is not uniform. As seen in (fig 11b), | the pulse pattern can be seen, the magnitude and duration of each pulse is not uniform. As seen in (fig 11b), | ||
the length of active expression time in the intermediate steps (ED2 and HG2) is considerably shorter, as | the length of active expression time in the intermediate steps (ED2 and HG2) is considerably shorter, as | ||
Revision as of 19:45, 1 November 2017
Model
Overview
We believe that mathematical modeling is fundamental to synthetic biology, and this is why we have decided to characterise recombination as comprehensively as possible. To achieve this, we split it into four parts. First, we compare how the deterministic and stochastic models simulate our recombinase-expressing E. coli strains. Second, we use our stochastic model to predict recombination efficiency and apply it to help witht the model of the Technion Israel iGEM team. Third, we combine the above two models together to perform in silico experiments for our pulse generators. Finally, we have built tools based on literature to estimate the number of off-target recombination sites inside a genome, as well as to predict the effect of distance between two target sites on the rate of recombination.
Modeling the expression of recombinase in E. coli
In our project, we used the BL21 DE3 E. coli strain transformed with two plasmids, one being T7-LacO regulated recombinase expression construct in pET28b, a medium copy plasmid (10~15), another one being Promoter-LoxP-Terminator-LoxP-RFP in pSB3C5, a low copy plasmid (~5):

As shown above, the LacI protein inhibitor is constitutively expressed, which dimerizes and binds to the operon regions controlling the expression of T7 polymerase and Cre recombinase. Without IPTG, we expect no T7 polymerase and Cre to be expressed. Without Cre recombinase being expressed, the terminator upstream of the RFP will not be excised, hence, in the absence of IPTG we expect minimal expression of RFP. First, we run the model and determine the amount of LacI inhibitor, LacY permease, and T7 polymerase in equilibrium at its constitutive state. Using these values as the initial values, we then add the T7-LacO-Cre plasmid and the P-LTL-RFP plasmid into the model, and determine the amount of leaky RFP production in the absence of IPTG, and the amount of RFP production in the presence of IPTG at various concentrations and induction time.
Setting the parameters
We based our LacI-LacY induction model on the paper by Stamatakis and Mantzaris in 2009 [1]. As both T7 and LacY in our model are regulated by LacI-LacO interaction, the parameters of T7 transcription and translation are treated as identical to LacY. Similarly, Cre transcription and translation is similar to that of the T7, except Cre transcription requires T7 polymerase, which we include in our list of equations. The second part of our model concerns the how Cre recombinase mediates recombination, which is based on the paper by Shoura et al. in 2012 [2]. We have adopted the rate constants determined by Shoura et al. [2] and Ringrose et el. [3] in a series of in vitro experiments.
Details of the parameters, chemical species, and chemical reactions are listed in the appendix at the bottom of the page. We used Python to run both the deterministic and stochastic simulations. For the most-up-to-date information on our modelling codes, click the provided GitHub links. For judging purposes, download the attached zip file, where you can obtain all relevant code and instructions that have been hosted on the iGEM servers.
Click hereto access our code for deterministic model, and herefor the stochastic model in github.
Amount of LacI and T7 in uninduced E. coli
Figures 2 and 3 show the change of LacI, LacY, and T7 copy number over time in a single E. coli cell.


As shown, the level of LacI dimer, the functional unit for repressing LacY and T7 expression, stabilizes at about 2,000 copies per cell, in both the deterministic and stochastic models. The levels of LacY and T7 stabilize at about 4 copies per cell for the deterministic model. The probabilistic nature of T7-LacO regulation is highlighted in the stochastic modeling, where after averaging 10 iterations, the level of LacY and T7 stabilizes at 4 copies and 0 copy respectively.
Amount of Cre recombinase and RFP in uninduced E. coli
Figure 4 below shows the level of RFP in uninduced E. coli estimated by deterministic simulation, whereas figure 5 shows the results of stochastic simulation:

We can see significantly different behaviour between the deterministic and the stochastic models. Whereas the behaviour of a single stochastic simulation (fig. 5a) is similar to that of the deterministic model (fig. 4) – showing a peak from a burst of gene expression while stabilizing at a lower level, averaging the iterations of stochastic models (fig. 5b) shows a steady increase of RFP level before plateauing. We can also see that the behaviour of each stochastic simulation – essentially the behaviour of individual cells – can vary drastically (fig. 6). Although only the plots of the stochastic model is shown (fig. 7), both models are able to predict that the leaky expression of T7 is significant enough to allow Cre to be expressed stably at about 14 copies per cell, a level sufficient for recombination, excising the LTL to allow the expression of RFP.


The results obtained here provide us with two pieces of information that we could be integrated into the wet lab, and guide us for future work:
First, an E. coli strain expressing more stringent control of protein expression should be used in place of BL21 (DE3). For example, strains (such as Lemo21 (DE3)) with pLysS expressing lysY , a T7 polymerase inhibitor, could minimize the leaky expression of Cre. Nevertheless, it turns out that this could not completely eliminate leaky recombination, as increasing the degradation rate of T7 polymerase by 1,000 times can still lead to RFP expression, although it lengthens the time required to reach equilibrium, indicating that pLysS can indeed lower the probability of leaky expression (Fig. 8). Thus, on top of changing E. coli host, in the future we should clone the Cre-expressing construct into a plasmid with even lower copy number, and also introduce degradation tags to the mRNA of Cre and to the Cre recombinase itself.

Second, stochastic modelling can better simulate the behaviour of biological systems with low copy number. In fact, by performing the simulation without iteration, we can generate completely behaviour that can mimic the ‘chance effect’ of leaky expression (fig. 6). As shown in the next section, stochastic modelling also performs better for simulating recombination. Therefore, we have chosen to use stochastic simulation to perform our in silico experiments for the pulse generator.
Recombination activity in E. coli
We performed simulation to model the expression of RFP under the induction of IPTG in various concentrations (100 mM, 400 mM, and 800 mM) using the deterministic model. Stochastic modelling is not suitable to model IPTG induction because it lacks the computational power required to simulate a high amount of IPTG. As shown, the recombination efficiency by Cre recombinase is very high, to a degree that recombination progression reaches equilibrium quickly regardless of the concentration of IPTG used to induce the expression of Cre recombinase (fig. 9). In fact, the pattern is similar to the uninduced E. coli (fig. 9d), further highlighting the need for a more stringent control of Cre expression.

Stochastic simulations were performed to model recombination, using a defined initial values of the copy number of Cre recombinase. We can see that, the recombination is very efficient, such that the difference in recombination rate is indistinguishable across three orders of magnitude difference of Cre recombinase copy number (fig. 10)

Interestingly, at equilibrium, stochastic model predicts that the recombination proceeds toward completion to a greater extent. Whereas in the deterministic model, six out of ten copies of P-LTL-RFP plasmid underwent recombination, nine out of ten copies underwent recombination in the stochastic model, even though all the parameters are identical.
In silico experiment of the pulse generator
Using the stochastic model, we built the pulse generator to simulate and the behaviour of our pulse generator. As shown above, the recombination proceeds relatively efficiently regardless of the actual recombinase protein copy number. Hence, in our stochastic model, we set the first site-specific recombinase to have an initial non-zero value (100 copies is used here), and track the behaviour of the pulse generator in the case of i) genome-integrated pulse generator, and ii) pulse generator in a medium-copy plasmid (10 copies).
Here, we have built a pulse generator with six recombinases, C, V, D, G, J, W, catalysing five recombination reactions. C binds to the L sites, excising the terminator between L_L to express V. V then binds to the M sites, excising the terminator between M_M to express D. To simplify the model and to decrease the computational load, we have split the pulse generator into individual ‘plasmids’. When the recombination for the n+2 plasmid is complete, it quickly degrades the nth plasmid, as if the recombination reaction at the n+2th step excise the expression construct at the nth step. This is done by adding a set of ‘artificial reactions’ – when D reacts with N_N (the 3rd plasmid), its recombination product quickly catalyzes the degradation of the recombination product of L_L (the 1st plasmid). The same principle applies for G and O_O, J and R_R, W and X_X, which degrades the recombination product of M_M, N_N, and O_O respectively.
Setting the parameters
For recombination, the rate constants follow that from the above. For the mRNA degradation rate, we have used 6.8 minute (408 seconds) as an estimate of their half-life, adopted from a paper analysing the global mRNA turnover rate in E. coli [4], and the translation rate is set by multiplying the mRNA degradation rate by the burst factor (b), which defines the average number of protein molecules produced per mRNA molecule [5]. Finally, the transcription rate is set to 0.01 s-1 and the protein half-life to 90 minutes.
A single module of recombination is shown in the appendix below. The full code of the pulse generator can be accessed through here in github. Alternatively this information can be found in the zip file at the top of the page, which is hosted on the iGEM servers.
Results
The pulse generator can temporally separate the metabolic burden of expressing multiple heterologous proteins
The panel below shows the pattern of expression of the four recombinases (V, D, G, J) and the level of the recombination products (PC2, AV2, ED2, HG2, TJ2, YW2) under default condition, where the pulse generator is genome-integrated, and in the condition when the pulse generator is in a plasmid of 10 copies (fig. 11). The last recombinase (W) is not shown, as being the last recombinase, its expression construct will not be excised and its expression level will be considerably higher than the rest.

We can see that under the default state, the pulse generator completes all the steps within 2.5 hours. Although the pulse pattern can be seen, the magnitude and duration of each pulse is not uniform. As seen in (fig 11b), the length of active expression time in the intermediate steps (ED2 and HG2) is considerably shorter, as the peaks do not reach as high as the other steps. This is further confirmed by (fig 11a), where we can see the expression of G and J are lower than those from the earlier steps (V and D). Nevertheless, we can clearly see that the pulse generator is able to temporally separate the transcription and translation of different genes, and with a high protein turnover rate, multiple species of proteins can be present inside the same cell, catalyzing a metabolic pathway, without utilizing too much resource due to excessive transcription and translation. Interestingly, in the case where there are 10 copies of the pulse generator, the pulsation progresses faster than the case where only one copy is present (fig. 11b and 11d). This might be due to the fact that recombination is highly efficient, so that with 10 copies, the recombinases are being expressed at a quicker pace, excising the previous construct faster. This also explains why the peak protein level is less than ten times higher than the case where only one pulse generator is present.
Lowering burst factor allows for better temporal separation
We then tested the effect of changing the burst factor (b) on the behaviour of the pulse generator (fig. 12 and 13). In both genome-integration and plasmid cases, doubling the burst rate speeds up both the progression of the pulse generator, and increases the peak protein amount, whereas halving the burst factor has the opposite effect.


More importantly, halving burst factor lengthens the expression time of the recombinases at the intermediate steps. This can be seen by comparing fig. 12d and fig. 12e, and fig. 13d and fig. 13e, where the expression of G and J are higher when the burst factor is lower. Therefore, we predict that in using the pulse generator for metabolic engineering, a lower burst factor is more desirable for the expression of recombinase. This can be achieved by using a less efficient ribosome binding site (RBS). Coupling the inefficient recombinase-expression construct with an efficient metabolic gene-expressor would allow good temporal separation of strong pathway enzyme expressions.
Identifying off-target sites in a genome
It is well-known that there exist sequences in the mammalian genome that Cre recombinase can recognize, and these can cause unwanted genetic modification events, leading to outcomes such as infertility [6] and growth defects [7]. Is is therefore important to identify potential target sites in a genome before using SMORE. To address this, we have adopted the program produced by Surendranath et al. [8] and used it to scan across the E. coli genome. We aim to use this program for two functions: i) Similar to the SeLOX [8], to search for cryptic target sites for a particular recombinase; ii) To determine the number of sites that the recombinase has binding affinity, and use it to estimate or adjust the rate constant of recombinase binding and dissociating to our desire target sites (see below)
Method
We have collected a list of sites that Cre can bind onto (but not necessary able to perform recombination) through literature search (See appendix), and used it to create a position weight matrix (PWM) (fig. 14). We then used the PWM to scan through the entire genome of E. coli BL21 (DE3), assigning score for each 13 base-pair sequence according to the PWM.
The Java program from which we used to generate the PWM and to scan the genome can be found here in github.
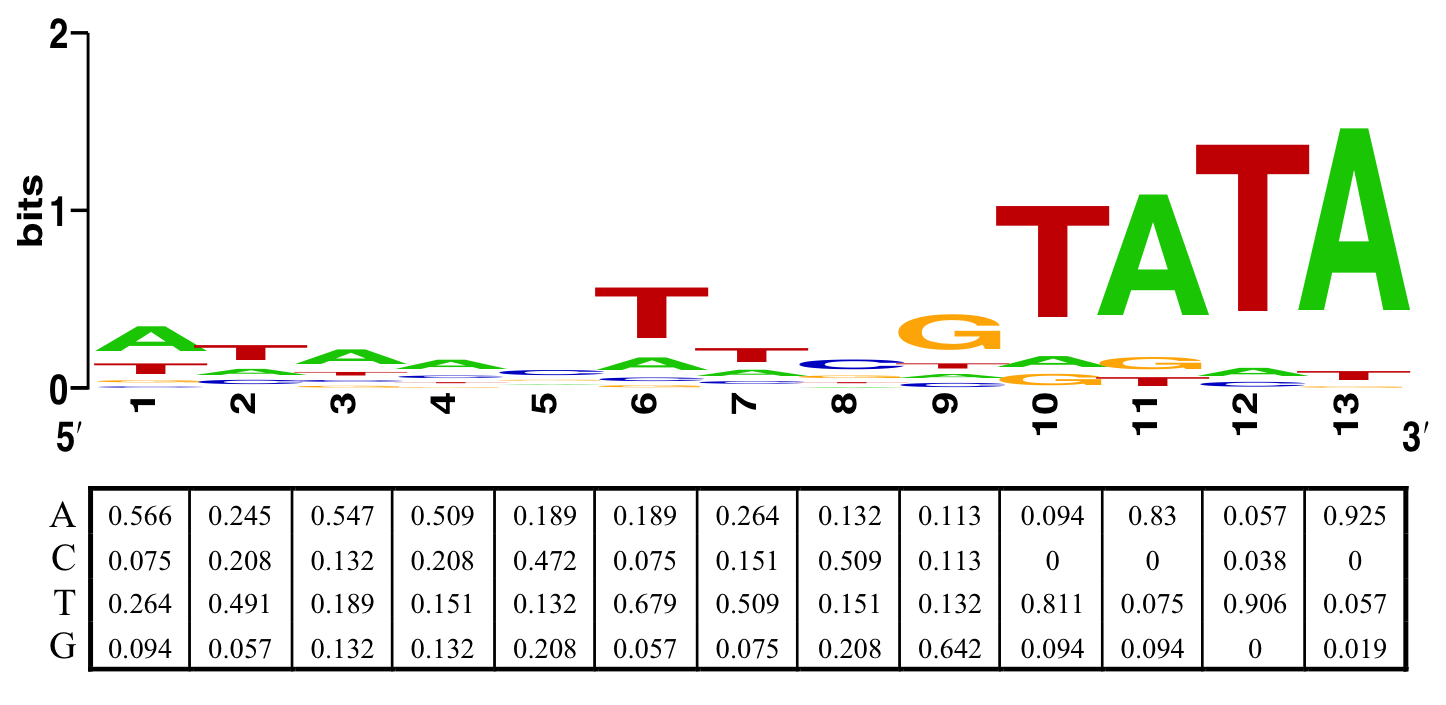
Identifying cryptic functional target sites in E. coli
We have modified our PWM to screen for potential complete and functional (34 bp) Cre recombinase target site within the E. coli genome. This is done by extending the PWM to include the second Cre binding site, separated by 8 bp from the first one. Since Cre is shown to tolerate 5 bp mutation in a 13 bp sequence [22], we define a functional Cre target site by having a score larger or equal to $(13-5)\times2 = 16$, with a normal LoxP site having a score of $13\times2 = 26$.
Using this method, we have identified 7691 potential LoxP sites within the genome of E. coli BL21 DE3. Of these 7691 sites, there are five of them with score above 20, and they are thus theoretically have the highest chance to be a functionally active Cre target sites. The table below shows their sequences and their location in the genome of E. coli BL21 (DE3), sequence ID: CP001509.3:
| Sequence | Genomic region | Nearby gene |
|---|---|---|
| CTAATTTAATATATTGATATTTATATCATTTTAC | 791275 to 791308 | YbhB and a putative ncRNA |
| ACAACTCTGTTTAAACTCTGATACACGAATTATT | 1691491 to 1691524 | YdhQ and valV |
| ATAAGTTTTTATAAAATTAAATATAAGATTATGG | 1961852 to 1961885 | amn and yeeN |
| AATACTTGATATATCATCACCTATACCATTTGCA | 3494831 to 3494864 | within yhiJ |
| GAAAAATAGTATGAATAAGAATATACGAATTTTA | 3716666 to 3716699 | two hypothetical proteins |
Adjusting the rate constants through screening for genomic Cre binding sites
We have used the PWM to calculate the score of each Cre binding sites in the appendix, and used the lowest score as the threshold to define whether a sequence in E. coli BL21 (DE3) can stably associate with Cre or not. Using this score, we have identified 308244 sites in the genome that Cre could potentially bind onto.
To estimate the rate constants of Cre binding to a target site, we follow the method by Bintu et al [9] that estimates the probability that an RNA polymerase is associated with a genuine promoter at any time:
$$P(RNAP \ bound \ to \ a \ promoter) = {P \over N_{NS}}e^{-\Delta\epsilon_{pd} / k_BT}$$
Where $N_{NS}$ is the number of non-specific binding sites that we have determined, $P$ is the number of recombinase molecules, $\Delta\epsilon$ is the energy change when Cre binds to the DNA, which is estimated from Hin recombinase to be $0.104 \times k_BT$ [10], and $k_B$ and $T$ are the boltzmann constant and temperature respectively. From this equation, the probability that Cre is associated with a target site is calculated to be $2.924 \times 10^{-6}$. We can then use the probability to estimate the rate constant in our stochastic model.
Conclusion and future work
Although the program detects five putative Cre target sites, they remain to be tested experimentally. Furthermore, one can notice that the five target sites do not have palindromic 13 bp repeats, which is the case in native LoxP site. Although this property is not a strict requirement for recombination (e.g. Lox66-LoxP pair is a functional Cre recombination site), non-palindromic sequences have a greatly reduced efficiency to mediate recombination (e.g. Lox66-Lox71 pair is mostly inactive in vivo) [22]. In fact, our current algorithm of identifying potential recombination site does not take into the account of the degree of symmetry, and should be modified in the future.
Due to time constraint, we did not have time to incorporate our estimation on the probability that Cre binds onto the target site into our stochastic simulation. Also, we did not have time to incorporate the results of the cryptic lox sites into the probability estimation. Given that Cre can bind onto genuine LoxP site with very high affinity [3], we expect that the seven thousand sites identified may as well have a significantly higher affinity than non-specific binding, and may thus affect the probability of Cre binding to the true target site. In the future, this two effects should be accounted to provide a more accurate mathematical depiction of site-specific recombinases.
Finally, while the in silico experiment has demonstrated the functionality of the pulse generator and has provided us insight about the choices of biobricks (e.g. weak RBS should be used for recombinase gene, whereas metabolic enzyme can be coupled with strong RBS), it remained to be experimentally verified. This is especially important when our model assumed the six recombinases are completely orthogonal, which is rarely the cases as we have determined (see our results page for a heat map describing the orthogonality of different recombinases in E. coli). Unfortunately, we did not have time to assemble our own pulse generator and were therefore unable to test it.
References
[1] Stamatakis, M, Mantzaris, N.V. (2009) Comparison of Deterministic and Stochastic Models of the lac Operon Genetic Network. Biophysical journal. 96(3): 887-906.
[2] Shoura, M.J., Vetcher, A.A., Giovan, S.M., Bardai, F., Bharadwaj, A., Kesinger, M.R., Levene, S.D. (2012) Measurements of DNA-loop formation via Cre-mediated recombination. Nucleic Acids Research. 40(15): 7452-7464
[3] Ringrose, L., Lounnas, V., Ehrlich, L., Buchholz, F., Wade, R., Stewart, A.F. (1998) Comparative Kinetic Analysis of FLP and Cre Recombinases: Mathematical Models for DNA Binding and Recombination. Journal of Molecular Biology. 284: 363-384
[4] Selinger, D.W., Saxena, R.M., Cheung, K.J., Church, G.M., Rosenow, C. (2003) Global RNA Half-Life Analysis in Escherichia coli Reveals Positional Patterns of Transcript Degradation. Genome research. 13: 216-223
[5] Thattai, M., van Oudenaarden, A. (2001) Intrinsic noise in gene regulatory networks. PNAS. 98(15): 8614-8619
[6] Schmidt, E.E., Taylor, D.S., Prigge, J.R., Barnett, S., Capecchi, M.R. (2000) Illegitimate Cre-dependent chromosome rearrangements in transgenic mouse spermatids. PNAS. 97(25): 13702-13707
[7] Loonstra, A., Vooijs, M., Beverloo, H.B., Allak, B.A., van Drunen, E., Kanaar, R., Berns, A., Jonkers, J. (2001) Growth inhibition and DNA damage induced by Cre recombinase in mammalian cells. PNAS, 98(16): 9209-9214
[8] Surendranath, V., Chusainow, J., Hauber, J., Buchholz, F., Habermann, B.H. (2010) SeLOX--a locus of recombination site search tool for the detection and directed evolution of site-specific recombination systems. Nucleic acids research. 38 (suppl_2): W293-W298
[9] Bintu, L., Buchler, N.E., Garcia, H.G., Gerland, U., Hwa, T., Kondev, J., Phillips, R. (2005) Transcriptional regulation by the numbers: models. Current Opinion in Genetics & Development. 15(2): 116-124
[10] Martin, T., Woodbury, N.W. (2001) Thermodynamics of specific and non-specific DNA binding by two DNA-binding domains conjugated to fluorescent probes. Biophysical Journal. 81(3): 1793-1804
[11] Thyagarajan, B., Guimarães, M.J., Groth, A.C., Calos, M.P. (2000) Mammalian genomes contain active recombinase recognition site. Gene. 244(1-2): 47-54
[12] Abremski, K., Hoess, R. (1985) Phage P1 Cre-loxP site-specific recombination: Effects of DNA supercoiling on catenation and knotting of recombinant products. Journal of Molecular Biology. 184(2): 211-220
[13] Albert, H., Dale, E.C., Lee, E., OW, D.W. (1995) Site-specific integration of DNA into wild-type and mutant lox sites placed in the plant genome. The Plant Journal. 7(4): 649-659
[14] Sauer, B. (1996) Multiplex Cre/lox recombination permits selective site-specific DNA targeting to both a natural and an engineered site in the yeast genome. Nucleic Acids Research. 24(23): 4608-4613
[15] Sauer, B. (1992) Identification of cryptic lox sites in the yeast genome by selection for Cre-mediated chromosome translocations that confer multiple drug resistance. Journal of Molecular Biology. 223(4): 911-928
[16] Araki, K., Okada, Y., Araki, M., Yamamura K-I. (2010) Comparative analysis of right element mutant lox sites on recombination efficiency in embryonic stem cells. BMC Biotechnology. 10:29
[17] Thomson, J.G., Rucker III, E.B., Piedrahita, J.A. (2003) Mutational analysis of loxP sites for efficient Cre-mediated insertion into genomic DNA. Genesis. 36(3): 162-167
[18] Sternberg, N., Hamilton, D., Hoess, R. (1981) Bacteriophage P1 site-specific recombination: II. Recombination between loxP and the bacterial chromosome. Journal of Molecular Biology. 150(4): 487-507
[19] Saraf-Levy, T., Santoro, S.W., Volpin, H., Kushnirsky, T., Eyal, Y., Schultz, P.G., Gidoni, D., Carmi, N. (2006) Site-specific recombination of asymmetric lox sites mediated by a heterotetrameric Cre recombinase complex. Bioorganic & Medicinal Chemistry. 14(9): 3081-3089
[20] Santoro, S.W., Schultz, P.G. (2002) Directed evolution of the site specificity of Cre recombinase. PNAS. 99(7): 4185-4190
[21] Buchholz, F., Stewart, A.F. (2001) Alteration of Cre recombinase site specificity by substrate-linked protein evolution. Nature Biotechnology. 19: 1047-1052
[22] Zhang, Z., Lutz, B. (2002) Cre recombinase‐mediated inversion using lox66 and lox71: method to introduce conditional point mutations into the CREB‐binding protein. Nucleic Acids Research. 30(17): e90
Appendix
List of chemical species:
| Symbol | Description |
|---|---|
| $$O_{T7}$$ | T7 polymerase gene, controlled by LacO operon |
| $$O_{Cre}$$ | Cre recombinase gene, controlled by LacO operon |
| $$O_{Y}$$ | LacY permease gene, controlled by LacO operon |
| $$O_{T7}R_2$$ | T7 polymerase gene, LacO operon bound by a LacI dimer |
| $$O_{Cre}R_2$$ | Cre recombinase gene, LacO operon bound by a LacI dimer |
| $$O_{Y}R_2$$ | LacY permease gene, LacO operon bound by a LacI dimer |
| $$M_R$$ | LacI mRNA |
| $$M_{T7}$$ | T7 polymerase mRNA |
| $$M_{Cre}$$ | Cre recombinase mRNA |
| $$M_Y$$ | LacY permease mRNA |
| $$M_{RFP}$$ | RFP mRNA |
| $$R$$ | LacI protein monomer |
| $$R_2$$ | LacI protein dimer |
| $$T7$$ | T7 polymerase protein |
| $$Cre$$ | Cre recombinase protein |
| $$LacY$$ | LacY permease protein |
| $$RFP$$ | RFP protein |
| $$I$$ | Intracellular IPTG |
| $$I_{ex}$$ | Extracellular IPTG |
| $$I_2R_2$$ | LacI dimer, sequestered by two IPTG molecules |
| $$YI_{ex}$$ | LacY permease bound to one extracellular IPTG molecule |
| $$S$$ | Substrate of Cre: A plasmid with LoxP-terminator-LoxP between promoter and RFP gene |
| $$SCre$$ | Substrate with one Cre molecule bound to one LoxP site |
| $$SCre^{(a)}_2$$ | Substrate with one Cre molecule bound to each LoxP sites |
| $$SCre^{(b)}_2$$ | Substrate with two Cre molecules bound to one LoxP site |
| $$SCre_3$$ | Substrate with three Cre molecules bound to the two LoxP sites |
| $$SCre_4$$ | Substrate with four Cre molecules bound to the two LoxP sites |
| $$SC$$ | Recombination intermediate |
| $$PCre_2$$ | Recombination product, with two Cre molecules bound to the LoxP site |
| $$PCre$$ | Recombination product, with one Cre molecule bound to the LoxP site |
| $$P$$ | Recombination product, with no Cre molecule bound to the LoxP site |
| $$QCre_2$$ | Recombination byproduct, with two Cre molecules bound to the LoxP site |
| $$QCre$$ | Recombination byproduct, with one Cre molecule bound to the LoxP site |
| $$Q$$ | Recombination byproduct, with no Cre molecule bound to the LoxP site |
List of parameters:
| Constant | Value | Unit | Description |
|---|---|---|---|
| $$k_{sMR}$$ | $$24.67^{*}$$ | $$nM min^{-1}$$ | Transcription rate of LacI-mRNA, constitutive promoter |
| $$\lambda_{MR}$$ | $$0.462$$ | $$min^{-1}$$ | Degradation rate of LacI-mRNA |
| $$k_{sR}$$ | $$15$$ | $$min^{-1}$$ | Translation rate of LacI protein |
| $$\lambda_{R}$$ | $$0.2$$ | $$min^{-1}$$ | Degradation rate of LacI protein |
| $$k_{2R}$$ | $$50$$ | $$nM^{-1} min^{-1}$$ | Dimerization rate of LacI monomer |
| $$k_{-2R}$$ | $$10^{-3}$$ | $$min^{-1}$$ | Dissociation rate of LacI dimer |
| $$k_{rT7}$$ | $$960$$ | $$nM^{-1} min^{-1}$$ | Binding constant, LacI dimer and T7 LacO |
| $$k_{-rT7}$$ | $$2.4$$ | $$min^{-1}$$ | Unbinding constant, LacI dimer and T7 LacO |
| $$k_{rY}$$ | $$960$$ | $$nM^{-1} min^{-1}$$ | Binding constant, LacI dimer and LacY LacO |
| $$k_{-rY}$$ | $$2.4$$ | $$min^{-1}$$ | Unbinding constant, LacI dimer and LacY LacO |
| $$k_{rCre}$$ | $$960$$ | $$nM^{-1} min^{-1}$$ | Binding constant, LacI dimer and Cre LacO |
| $$k_{-rCre}$$ | $$2.4$$ | $$min^{-1}$$ | Unbinding constant, LacI dimer and Cre LacO |
| $$\lambda_{R2}$$ | $$0.2$$ | $$min^{-1}$$ | Degradation rate of LacI dimer |
| $$k_{dr1}$$ | $$3\times10^{-7}$$ | $$nM^{-2}min^{-1}$$ | Rate constant of forming IPTG-LacI dimer |
| $$k_{-dr1}$$ | $$12$$ | $$min^{-1}$$ | Rate constant of dissociating IPTG-LacI dimer |
| $$k_{dr2}$$ | $$3\times10^{-7}$$ | $$nM^{-2}min^{-1}$$ | Rate constant, IPTG displacing LacI dimer from the T7 LacO |
| $$k_{-dr2}$$ | $$4.8\times10^3$$ | $$min^{-1}$$ | Rate constant, IPTG-LacI binding to empty T7 LacO, releasing two IPTG molecules |
| $$k_{rCre}$$ | $$960$$ | $$nM^{-1}min^{-1}$$ | Binding constant, LacI dimer and Cre LacO |
| $$k_{-rCre}$$ | $$2.4$$ | $$min^{-1}$$ | Unbinding constant, LacI dimer and Cre LacO |
| $$k_{dr3}$$ | $$3\times10^{-7}$$ | $$nM^{-2}min^{-1}$$ | Rate constant, IPTG displacing LacI dimer from the Cre LacO |
| $$k_{-dr3}$$ | $$4.8\times10^3$$ | $$min^{-1}$$ | Rate constant, IPTG-LacI binding to empty Cre LacO, releasing two IPTG molecules |
| $$\lambda_{I2R2}$$ | $$0.2$$ | $$min^{-1}$$ | Degradation rate of $IPTG_2-LacI_2$ |
| $$k_{s0MT7}$$ | $$0.01$$ | $$min^{-1}$$ | Leaky transcription rate of T7 mRNA (LacI bound) |
| $$k_{s1MT7}$$ | $$0.5$$ | $$min^{-1}$$ | Transcription rate of T7 mRNA (empty LacO) |
| $$\lambda_{MT}$$ | $$0.462$$ | $$min^{-1}$$ | Degradation rate of T7 mRNA |
| $$k_{sT7}$$ | $$30$$ | $$min^{-1}$$ | Translation rate of T7 protein |
| $$\lambda_{T7}$$ | $$0.2$$ | $$min^{-1}$$ | Degradation rate of T7 protein |
| $$k_{s0MCre}$$ | $$0.01$$ | $$min^{-1}$$ | Leaky transcription rate of Cre mRNA (LacI bound) |
| $$k_{s1MCre}$$ | $$0.5$$ | $$min^{-1}$$ | Transcription rate of Cre mRNA (empty LacO) |
| $$\lambda_{MCre}$$ | $$0.462$$ | $$min^{-1}$$ | Degradation rate of Cre mRNA |
| $$k_{sCre}$$ | $$30$$ | $$min^{-1}$$ | Translation rate of Cre protein |
| $$\lambda_{Cre}$$ | $$0.2$$ | $$min^{-1}$$ | Degradation rate of Cre protein |
| $$k_{s0MY}$$ | $$0.01$$ | $$min^{-1}$$ | Leaky transcription rate of LacY mRNA (LacI bound) |
| $$k_{s1MY}$$ | $$0.5$$ | $$min^{-1}$$ | Transcription rate of LacY mRNA (empty LacO) |
| $$k_{p}$$ | $$0.12$$ | $$nM^{-1}min^{-1}$$ | Association rate, external IPTG binding to LacY permease |
| $$k_{-p}$$ | $$0.1$$ | $$min^{-1}$$ | Dissociation rate between LacY permease and bound IPTG |
| $$k_{ft}$$ | $$6\times10^4$$ | $$min^{-1}$$ | Import rate of IPTG by facilitated transport |
| $$k_{t}$$ | $$6\times10^4$$ | $$min^{-1}$$ | Rate of IPTG transport by passive diffusion |
| $$k_{1}$$ | $$13.2$$ | $$nM^{-1}min^{-1}$$ | Association rate of Cre to empty LoxP site |
| $$k_{-1}$$ | $$3.96$$ | $$min^{-1}$$ | Dissociation rate of Cre from a LoxP site with only one Cre molecule bound |
| $$k_{2}$$ | $$13.5$$ | $$nM^{-1}min^{-1}$$ | Association rate of Cre to a LoxP site already occupied with one Cre molecule |
| $$k_{-2}$$ | $$0.288$$ | $$min^{-1}$$ | Dissociation rate of Cre from a LoxP site with two Cre molecule bound |
| $$k_{3}$$ | $$2.4$$ | $$min^{-1}$$ | Formation rate of recombination complex |
| $$k_{-3}$$ | $$13$$ | $$min^{-1}$$ | Disassembly rate of recombination complex |
| $$k_{4}$$ | $$0.021$$ | $$min^{-1}$$ | Rate of recombination |
| $$k_{-4}$$ | $$10$$ | $$nM^{-2}min^{-1}$$ | Rate of recombination, reverse direction |
| $$k_{M_{RFP}}$$ | $$0.5$$ | $$min^{-1}$$ | Transcription rate of RFP mRNA |
| $$k_{RFP}$$ | $$30$$ | $$min^{-1}$$ | Translation rate of RFP protein |
| $$\lambda_{M_{RFP}}$$ | $$0.462$$ | $$min^{-1}$$ | Degradation rate of RFP mRNA |
| $$\lambda_{RFP}$$ | $$0.2$$ | $$min^{-1}$$ | Degradation rate of RFP protein |
List of reactions:
\[\phi \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_{sMR}}}_{\mathrm{\lambda_{MR}}}} M_R\] \[M_R \mathrel{\mathop{\rightarrow}^{\mathrm{k_{sR}}}} M_R + R\] \[2R \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_{2R}}}_{\mathrm{k_{-2R}}}} R_2\] \[O_Y + R_2 \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_{rY}}}_{\mathrm{k_{-rY}}}} O_YR_2\] \[O_{T7} + R_2 \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_{rT7}}}_{\mathrm{k_{-rT7}}}} O_{T7}R_2\] \[O_{Cre} + R_2 \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_{rCre}}}_{\mathrm{k_{-rCre}}}} O_{Cre}R_2\] \[2I + R_2 \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_{dr1}}}_{\mathrm{k_{-dr1}}}} R_2I_2\] \[O_YR_2 + 2I \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_{dr2}}}_{\mathrm{k_{-dr2}}}} O_Y + R_2I_2\] \[O_{T7}R_2 + 2I \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_{dr2}}}_{\mathrm{k_{-dr2}}}} O_{T7} + R_2I_2\] \[O_{Cre}R_2 + 2I \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_{dr2}}}_{\mathrm{k_{-dr2}}}} O_{Cre} + R_2I_2\] \[O_Y \mathrel{\mathop{\rightarrow}^{\mathrm{k_{s1MY}}}} O_Y + M_Y\] \[O_YR_2 \mathrel{\mathop{\rightarrow}^{\mathrm{k_{s0MY}}}} O_YR_2 + M_Y\] \[O_{T7} \mathrel{\mathop{\rightarrow}^{\mathrm{k_{s1MT7}}}} O_{T7} + M_{T7}\] \[O_{T7}R_2 \mathrel{\mathop{\rightarrow}^{\mathrm{k_{s0MT7}}}} O_{T7}R_2 + M_{T7}\] \[O_{Cre} + T7 \mathrel{\mathop{\rightarrow}^{\mathrm{k_{s1MCre}}}} O_{Cre} + T7 + M_{Cre}\] \[O_{Cre}R_2 + T7 \mathrel{\mathop{\rightarrow}^{\mathrm{k_{s0MCre}}}} O_{Cre}R_2 + T7 + M_{Cre}\] \[M_Y \mathrel{\mathop{\rightarrow}^{\mathrm{k_{sY}}}} M_Y + LacY\] \[M_{T7} \mathrel{\mathop{\rightarrow}^{\mathrm{k_{sT7}}}} M_{T7} + T7\] \[M_{Cre} \mathrel{\mathop{\rightarrow}^{\mathrm{k_{sCre}}}} M_{Cre} + Cre\] \[LacY + I_{ex} \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_p}}_{\mathrm{k_{-p}}}} YI_{ex}\] \[YI_{ex} \mathrel{\mathop{\rightarrow}^{\mathrm{k_{ft}}}} LacY + I\] \[I_{ex} \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_t}}_{\mathrm{k_t}}} I\] \[M_Y \mathrel{\mathop{\rightarrow}^{\mathrm{\lambda_{MY}}}} \phi \] \[M_{T7} \mathrel{\mathop{\rightarrow}^{\mathrm{\lambda_{M_{T7}}}}} \phi \] \[M_{Cre} \mathrel{\mathop{\rightarrow}^{\mathrm{\lambda_{M_{Cre}}}}} \phi \] \[LacY \mathrel{\mathop{\rightarrow}^{\mathrm{\lambda_{Y}}}} \phi \] \[T7 \mathrel{\mathop{\rightarrow}^{\mathrm{\lambda_{T7}}}} \phi \] \[Cre \mathrel{\mathop{\rightarrow}^{\mathrm{\lambda_{Cre}}}} \phi \] \[S + Cre \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_1}}_{\mathrm{k_{-1}}}} SCre\] \[SCre + Cre \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_1}}_{\mathrm{k_{-1}}}} SCre^{(a)}_2\] \[SCre + Cre \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_2}}_{\mathrm{k_{-2}}}} SCre^{(b)}_2\] \[SCre^{(a)}_2 \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_2}}_{\mathrm{k_{-2}}}} SCre_3\] \[SCre^{(b)}_2 \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_1}}_{\mathrm{k_{-1}}}} SCre_3\] \[SCre_3 \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_2}}_{\mathrm{k_{-2}}}} SCre_4\] \[SCre_4 \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_3}}_{\mathrm{k_{-3}}}} SC\] \[SC \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_4}}_{\mathrm{k_{-4}}}} PCre_2 + QCre_2\] \[PCre_2 \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_{-2}}}_{\mathrm{k_{2}}}} PCre + Cre\] \[PCre \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_{-1}}}_{\mathrm{k_{1}}}} P + Cre\] \[QCre_2 \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_{-2}}}_{\mathrm{k_{2}}}} QCre + Cre\] \[QCre \mathrel{\mathop{\rightleftharpoons}^{\mathrm{k_{-1}}}_{\mathrm{k_{1}}}} Q + Cre\] \[PCre_2 \mathrel{\mathop{\rightarrow}^{\mathrm{k_{M_{RFP}}}}} PCre_2 + M_{RFP}\] \[PCre \mathrel{\mathop{\rightarrow}^{\mathrm{k_{M_{RFP}}}}} PCre + M_{RFP}\] \[P \mathrel{\mathop{\rightarrow}^{\mathrm{k_{M_{RFP}}}}} P + M_{RFP}\] \[M_{RFP} \mathrel{\mathop{\rightarrow}^{\mathrm{k_{RFP}}}} M_{RFP} + RFP\] \[M_{RFP} \mathrel{\mathop{\rightarrow}^{\mathrm{\lambda_{M_{RFP}}}}} \phi \] \[RFP \mathrel{\mathop{\rightarrow}^{\mathrm{\lambda_{RFP}}}} \phi \]
Differential Equations
\begin{equation} \frac{d[M_R]}{dt} = k_{sMR} - \lambda_{MR}[M_R] \end{equation} \begin{equation} \frac{d[R]}{dt} = k_{sR}[M_R] - 2k_{2R}[R]^2 + 2k_{-2R}[R_2] - \lambda_R[R] \end{equation} \begin{equation} \frac{d[R_2]}{dt} = k_{2R}[R]^2 - k_{-2R}[R_2] - k_{rT7}[R_2][O_{T7}] + k_{-rT7}([O_{T7}]_T-[O_{T7}]) - k_{rY}[R_2][O_Y] + k_{-rY}([O_Y]_T-[O_Y]) \\ - k_{rCre}[R_2][O_{Cre}] + k_{-rCre}([O_{Cre}]_T-[O_{Cre}]) - k_{dr1}[I]^2[R_2] + k_{-dr1}[I_2R_2] - \lambda_{R_2}[R_2]] \end{equation} \begin{equation} \frac{d[O_Y]}{dt} = - k_{rY}[R_2][O_Y] + k_{-rY}([O_Y]_T-[O_Y]) + k_{dr4}[I]^2([O_Y]_T-[O_Y]) - k_{-dr4}[I_2R_2][O_Y] \end{equation} \begin{equation} \frac{d[O_{T7}]}{dt} = - k_{rT7}[R_2][O_{T7}] + k_{-rT7}([O_{T7}]_T-[O_{T7}]) + k_{dr2}[I]^2([O_{T7}]_T-[O_{T7}]) - k_{-dr2}[I_2R_2][O_{T7}] \end{equation} \begin{equation} \frac{d[O_{Cre}]}{dt} = - k_{rCre}[R_2][O_{Cre}] + k_{-rCre}([O_{Cre}]_T-[O_{Cre}]) + k_{dr3}[I]^2([O_{Cre}]_T-[O_{Cre}]) - k_{-dr3}[I_2R_2][O_{Cre}] \end{equation} \begin{equation} \frac{d[I]}{dt} = -2k_{dr1}[I]^2[R_2] + 2k_{-dr1}[I_2R_2] - 2k_{dr2}[I]^2([O_{T7}]_T-[O_{T7}]) + 2k_{-dr2}[I_2R_2][O_{T7}] - 2k_{dr3}[I]^2([O_{Cre}]_T-[O_{Cre}]) \\ + 2k_{-dr3}[I_2R_2][O_{Cre}] - 2k_{dr4}[I]^2([O_Y]_T-[O_Y]) + 2k_{-dr4}[I_2R_2][O_Y] + k_{ft}[YI_{ex}] + k_t([I_{ex}]-[I]) + 2\lambda_{I_2R_2}[I_2R_2] + \lambda_{YI_{ex}}[YI_{ex}] \end{equation} \begin{equation} \frac{d[I_2R_2]}{dt} = k_{dr1}[I]^2[R_2] - k_{-dr1}[I_2R_2] + k_{dr2}[I]^2([O_{T7}]_T-[O_{T7}]) - k_{-dr2}[I_2R_2][O_{T7}] + k_{dr3}[I]^2([O_{Cre}]_T-[O_{Cre}]) \\ - k_{-dr3}[I_2R_2][O_{Cre}] + k_{dr4}[I]^2([O_Y]_T-[O_Y]) - k_{-dr4}[I_2R_2][O_Y] - \lambda_{I_2R_2}[I_2R_2] \end{equation} \begin{equation} \frac{d[M_Y]}{dt} = k_{s0MY}([O_Y]_T-[O_Y]) + k_{s1MY}[O_Y] - \lambda_{MY}[M_Y] \end{equation} \begin{equation} \frac{d[LacY]}{dt} = k_{sY}[M_Y] + (k_{ft} + k_{-p})[YI_{ex}] - k_p[LacY][I_{ex}] - \lambda_Y[LacY] \end{equation} \begin{equation} \frac{d[M_{T7}]}{dt} = k_{s0MT7}([O_{T7}]_T-[O_{T7}]) + k_{s1MT7}[O_{T7}] - \lambda_{M_{T7}}[M_{T7}] \end{equation} \begin{equation} \frac{d[T7]}{dt} = k_{sT7}[M_{T7}] - \lambda_{T7}[T_7] \end{equation} \begin{equation} \frac{d[M_{Cre}]}{dt} = k_{s0Mcre}([O_{Cre}]_T-[O_{Cre}])[T_7] + k_{s1Mcre}[O_{Cre}][T_7] - \lambda_{Mcre}[M_{Cre}] \end{equation} \begin{equation} \frac{d[Cre]}{dt} = k_{sCre}[M_{Cre}] - \lambda_{Cre}[Cre] - k_1[S][Cre] + k_{-1}[SCre] - k_1[SCre][Cre] + k_{-1}[SCre^{(a)}_2] - k_2[SCre][Cre] + k_{-2}[SCre^{(b)}_2] - \\ k_2[SCre^{(a)}_2][Cre] + k_{-2}[SCre_3] - k_1[SCre^{(b)}_2][Cre] + k_{-1}[SCre_3] - k_2[SCre_3][Cre] \\ + k_{-2}[SCre_4] + k_{-2}([QCre_2]+[PCre_2]) - k_2([QCre]+[PCre])[Cre] + k_{-1}([QCre]+[PCre]) - k_1([Q]+[P])[Cre] \end{equation} \begin{equation} \frac{d[YI_{ex}]}{dt} = - (k_{ft} + k_{-p})[YI_{ex}] + k_p[LacY][I_{ex}] - \lambda_{YI_{ex}}[YI_{ex}] \end{equation} \begin{equation} \frac{d[S]}{dt} = -k_1[S][Cre] + k_{-1}[SCre] \end{equation} \begin{equation} \frac{d[SCre]}{dt} = k_1[S][Cre] - k_{-1}[SCre] - (k_1 + k_2)[SCre][Cre] + k_{-1}[SCre^{(a)}_2] + k_{-2}[SCre^{(b)}_2] \end{equation} \begin{equation} \frac{d[SCre^{(a)}_2]}{dt} = k_1[SCre][Cre] - k_{-1}[SCre^{(a)}_2] - k_2[SCre^{(a)}_2][Cre] + k_{-2}[SCre_3] \end{equation} \begin{equation} \frac{d[SCre^{(b)}_2]}{dt} = k_2[SCre][Cre] - k_{-2}[SCre^{(b)}_2] - k_1[SCre^{(b)}_2][Cre] + k_{-1}[SCre_3] \end{equation} \begin{equation} \frac{d[SCre_3]}{dt} = k_2[SCre^{(a)}_2][Cre] - (k_{-2} + k_{-1})[SCre_3] + k_1[SCre^{(b)}_2][Cre] - k_2[SCre_3][Cre] + k_{-2}[SCre_4] \end{equation} \begin{equation} \frac{d[SCre_4]}{dt} = k_2[SCre_3][Cre] - (k_{-2} + k_3)[SCre_4] + k_{-3}[SC] \end{equation} \begin{equation} \frac{d[SC]}{dt} = k_3[SCre_4] - (k_{-3} + k_{-4})[SC] + k_4[QCre_2][PCre_2] \end{equation} \begin{equation} \frac{d[QCre_2]}{dt} = k_{-4}[SC] - k_4[QCre_2][PCre_2] - k_{-2}[QCre_2] + k_2[QCre][Cre] \end{equation} \begin{equation} \frac{d[PCre_2]}{dt} = k_{-4}[SC] - k_4[QCre_2][PCre_2] - k_{-2}[PCre_2] + k_2[PCre][Cre] \end{equation} \begin{equation} \frac{d[QCre]}{dt} = k_{-2}[QCre_2] - k_2[QCre][Cre] - k_{-1}[QCre] + k_1[Q][Cre] \end{equation} \begin{equation} \frac{d[PCre]}{dt} = k_{-2}[PCre_2] - k_2[PCre][Cre] - k_{-1}[PCre] + k_1[P][Cre] \end{equation} \begin{equation} \frac{d[Q]}{dt} = k_{-1}[QCre] - k_1[Q][Cre] \end{equation} \begin{equation} \frac{d[P]}{dt} = k_{-1}[PCre] - k_1[P][Cre] \end{equation} \begin{equation} \frac{d[M_{RFP}]}{dt} = k_{mRFP}([P] + [PCre] + [PCre_2]) - \lambda_{mRFP}[M_{RFP}] \end{equation} \begin{equation} \frac{d[RFP]}{dt} = k_{RFP}[M_{RFP}] - \lambda_{RFP}[RFP] \end{equation}
List of Cre-binding sites
| Target site | Sequence | Reference |
|---|---|---|
| LoxP | ATAACTTCGTATA | [11] |
| hXp22 (LE) | ACAACCATTTATA | [11] |
| hXp22 (RE) | ATAACATCATATA | [11] |
| FPSTR1 | AGAACCATTTATA | [11] |
| PSTR1 | GATACATCATATA | [11] |
| H7q21 (LE) | ATACATACGTATA | [11] |
| H7q21 (RE) | ATATATATGTATA | [11] |
| M5 (LE) | GTAACTGAGTATA | [11] |
| M5 (RE) | ATATATACGTATA | [11] |
| LoxΔ86 | GCCTCGAGGTATA | [12] |
| LoxΔ117 | CCTAGGCCCTATA | [12] |
| Lox43 | CTCGGTACCTATA | [13] |
| Lox44 | AATGCATGCTATA | [13] |
| Lox66 & Lox71 | TACCGTTCGTATA | [13], [16] |
| Lox76 & Lox75 | TACCGGGCGTATA | [13] |
| LoxFAS1 (LE) | TTGCCTTCGTATA | [14] |
| LoxFAS1 (RE) | ATTACTTGGTATA | [14] |
| Mock LoxFAS1 (LE) | TAAGCTTCGTATA | [14] |
| Class 1 | AAATTAGCTTATA | [15] |
| Class 2 | GCTCCAACATATA | [15] |
| Class 3 | AAAAAAAGGTATA | [15] |
| Class 4 | CTTCCTTCTTGTT | [15] |
| Class 5 | ACAAAAAAGAGTT | [15] |
| Class 6 | ACCATATAAGTTA | [15] |
| Class 7 | TTGCCTGTGGACA | [15] |
| Class 8 | CAAGCTTCGTATA | [15] |
| Class 9 | TTGGGTCATTATA | [15] |
| Class 10 | TATATTAATGATA | [15] |
| SerS (LE) | TTACCTTCGTATA | [15] |
| SerS (RE) | ACAAAAAAGAGTT | [15] |
| PUT4 (LE) | GCCATCTCCGTAA | [15] |
| PUT4 (RE) | TTGGGTCATTATA | [15] |
| LoxJTZ17 | ATAAATTGCTATA | [16] |
| LoxKR1 | AACAGTTGGTATA | [16] |
| LoxKR2 | TTAAGTTGGTATA | [16] |
| LoxKR3 | ATAACAAGGTATA | [16] |
| LoxKR4 | ATAACTTGCAATA | [16] |
| LoxJT15 | AATTATTCGTATA | [17] |
| LoxJT12 | AGTTGTTCGTATA | [17] |
| LoxJT510 | TAACGTTCGTATA | [17] |
| LoxJTZ2 | AGGTATTCGTATA | [17] |
| LoxR | TCGCTTCGGATAA | [18] |
| LoxL | TATGTTTCGGATA | [18] |
| LoxB | TCGCTTCGGATAA | [18] |
| LoxM7 | ATAACTCTATATA | [19] |
| M1 | ATAACTTCATATA | [20] |
| M2 | ATAACTTCGTACA | [20] |
| M4 | ATAACTTTGTATA | [20] |
| M6 | ATAACTCTGTATA | [20] |
| M8 | ATAACTCTGTGTA | [20] |
| LoxH | ATATATACGTATA | [21] |
| LoxM | ATAAGCTCGTGTG | [21] |
A single module of pulse generator
\begin{align} Cre + LL & \leftrightarrow LCL \\ Cre + LL & \leftrightarrow LLC \\ Cre + LCL & \leftrightarrow LC_2L\\ Cre + LCL & \leftrightarrow LCLC\\ Cre + LLC & \leftrightarrow LLC_2\\ Cre + LLC & \leftrightarrow LCLC\\ Cre + LC_2L & \leftrightarrow LC_2LC \\ Cre + LCLC & \leftrightarrow LC_2LC\\ Cre + LCLC & \leftrightarrow LCLC_2\\ Cre + LLC_2 & \leftrightarrow LCLC_2\\ Cre + LCLC_2 & \leftrightarrow S\\ Cre + LC_2LC & \leftrightarrow S\\ S & \leftrightarrow S^{star}\\ S^{star} & \leftrightarrow PC_2 + QC_2\\ PC_2 & \leftrightarrow PC + Cre\\ PC & \leftrightarrow P + Cre\\ QC_2 & \leftrightarrow QC + Cre\\ QC & \leftrightarrow Q + Cre\\ \end{align}











