Modelling PLP production
The problem
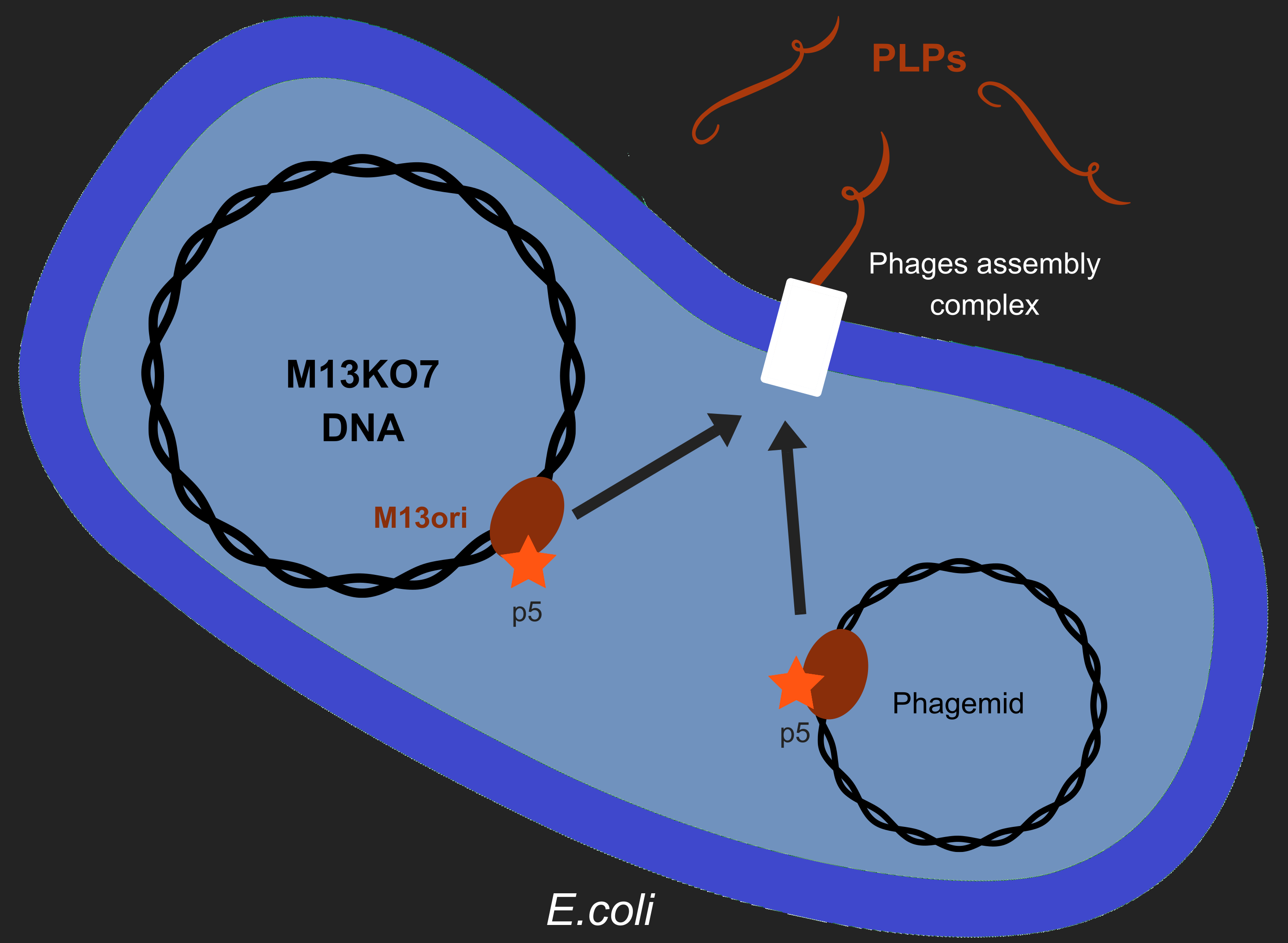
Our objective is to produce phage like particles (PLP), for this, the bacteria must contain both a helper phage and also a phagemid (Figure 1). During phage production, several key events determine which DNA molecules are packaged into phage or PLP. These involve recognition of the M13 replication origin by several phage proteins.
A major hurdle to marketing KILL XYL is obtaining the necessary authorizations. Our interviews and legislation study both showed that the number of viable phages could be a problem. We therefore decided to measure and model the ratio between viable phage and phage-like particles, and so try to optimize this ratio to facilitate the preparation of pure PLP.
The Model
We based our model on a recently published model of "wild-type" M13 replication [1] [2].
This model was modified to accommodate the fact our system has two plasmids (Helper and Phagemid) while the previously modeled system has only one. This means we incorporated: the presence of a phagemid, with its own replicative origin and M13 origin, the helper-phage E. coli plasmid origin and the modification of the helper-phage M13 origin. This was done by adapting the existing model and adding new parts to the existing model. These modifications added 9 species and 3 parameters and 13 equations to the original model, and changed 8 parts of the previous model.
We observed we could roughly reproduce the published copy number of plasmids by tweaking our parameter describing the affinity of DNA polymerase for the plasmid's origin of replication ("Polymerase Binding Event") in our model when the reactions describing phage formation where inactivated. This is a purely empirical observation. To the best of our knowledge, their is no published data describing this parameter, which is why we assumed published data for plasmid copy number can be used as a proxy to approximate the proclivity of DNA polymerase to bind the plasmid's origin of replication.
The modified model is available File:T--Aix-Marseille--Model.zip
We used the initial measurement to constrain parameters of the model.
Results
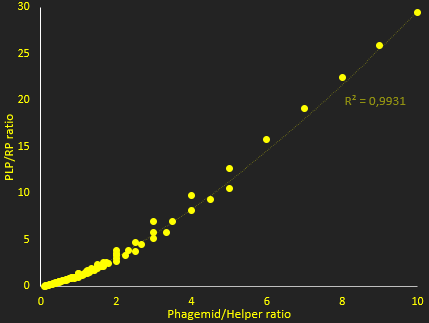
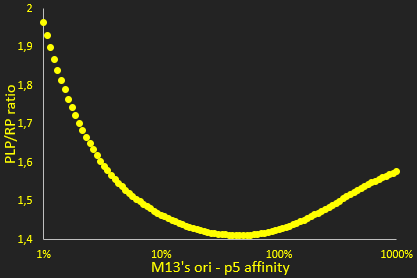
The packaging ratio depends on two main parameters: the initial ratio of transformed phagemid and helper phage (Figure 2), and the difference in p5 affinity for eitheir plasmid's M13 ori (Figure 3).
In figure 2, we investigate how the ratio of PLP to replicative phage depends on the copy number of the two plasmids used. This shows that higher copy numbers of phagemid increase this ratio. This simulation showed essentially that increasing copy number increases packaging efficiency, and ratio of PLP to phage. The resut hide however, that at very high ratios, the lack of protein reduces production. Nevertheless, and in view of this result for the tests we used a backbone that gives, in theory, a very high copy number for the phagemid, to try and maximize the ratio of PLP to phage.
The next parameter we investigated was the relative affinity of the phagemid and helper phage origins of replication for the p5 protein (Figure 3). This affinity is critical in the model for determining whether single-stranded DNA is used for packaging or making additional double-stranded DNA. This graph shows a clear minimum where the PLP to phage ratio is the least favorable. However, as we are interested in the left-hand part of the graph, the efficiency of the M13 origin can be reduced but not easily improved, we see that lower efficiencies improve the ratio. This result is not unexpected, like the previous ones for the ratio of helper phage to phagemid. Nevertheless, our results show a much lower sensitivity to this parameter than we initially expected.
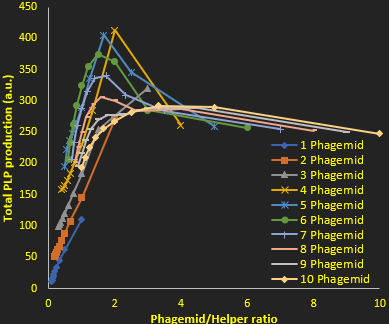
As we found above (figure 2), the higher the phagemid to helper phage ratio the better the PLP production. However this increased purity is offset by a drop in the amount of PLPs produced, due to a lack of proteins (which are encoded by the helper phage). This is why we also investigated the total PLP production as a function phagemid to helper ratio (Figure 4). This allowed us to determine the optimal conditions for maximal production of PLPs. Our results suggest that about 10 phagemids and 2 helper pahges per cell PLP production is optimized in the long term. This result allows us to redesign the origins of replication and selection presures to optimize PLP prodiction.
Conclusions
Our measurements show the initial design needs to be improved to increase the proportion of PLP produced. This is important to optimize production of PLP and facilitate purification. The model showed us that the most important parameters in determining the proportion of PLP produced are plasmid copy number and affinity between the M13 origin and protein p5, as shown in figures 2 and 3. However, plasmid copy number also plays a role in total PLP yield as shown in figure 4.
Our initial reaction, from early results, was to use a very high copy number plasmid, pBluescript, to ensure a maximal PLP to phage ratio. Experimentally this was not very effective as can be seen from our measurements.
The model we have made of PLP production suggests it is necessary to redesign certain features. Specifically, we should take into account the role played by plasmid copy number, and choose our backbones to ensure the right equilibrium between protein production and DNA production. The model suggests a ratio of about 5 so we should complement the p15A origin of M13KO7 with a phagemid with fewer copies than pBluescript.
In conclusion, our modeling modified our wet-lab approach by directing us towards pBluescript as a very high copy number plasmid, however more detailed analysis suggests that better results might be obtained with a different backbone equilibrating protein and DNA producition.
The mathematical model we have produced can clearly be improved, and aspects that we have not included, that deserve incorporation, are
- the influence of antibiotics on copy number for plasmids and phages containing a resistance cassette;
- the influence of replication origin on maintained copy number;
- the effects of M13 origin on duplication of phage RF.
- ↑ Smeal et al, Simulation of the M13 life cycle I: Assembly of a genetically-structured deterministic chemical kinetic simulation, Virology, 500, January 2017
- ↑ Smeal et al, Simulation of the M13 life cycle II: Investigation of the control mechanisms of M13 infection and establishment of the carrier state, Virology, 500, January 2017