Chemical Diffusion
Model
An experiment is designed to demonstrate that the genetic insertion does not damage the olfactory receptor neuron pairs. This is achieved by testing worms’ response to diacetyl and 2-nonanone. We assume that if the neuron pair is unaffected, the modified worms will respond to the chemicals as the wild types do.
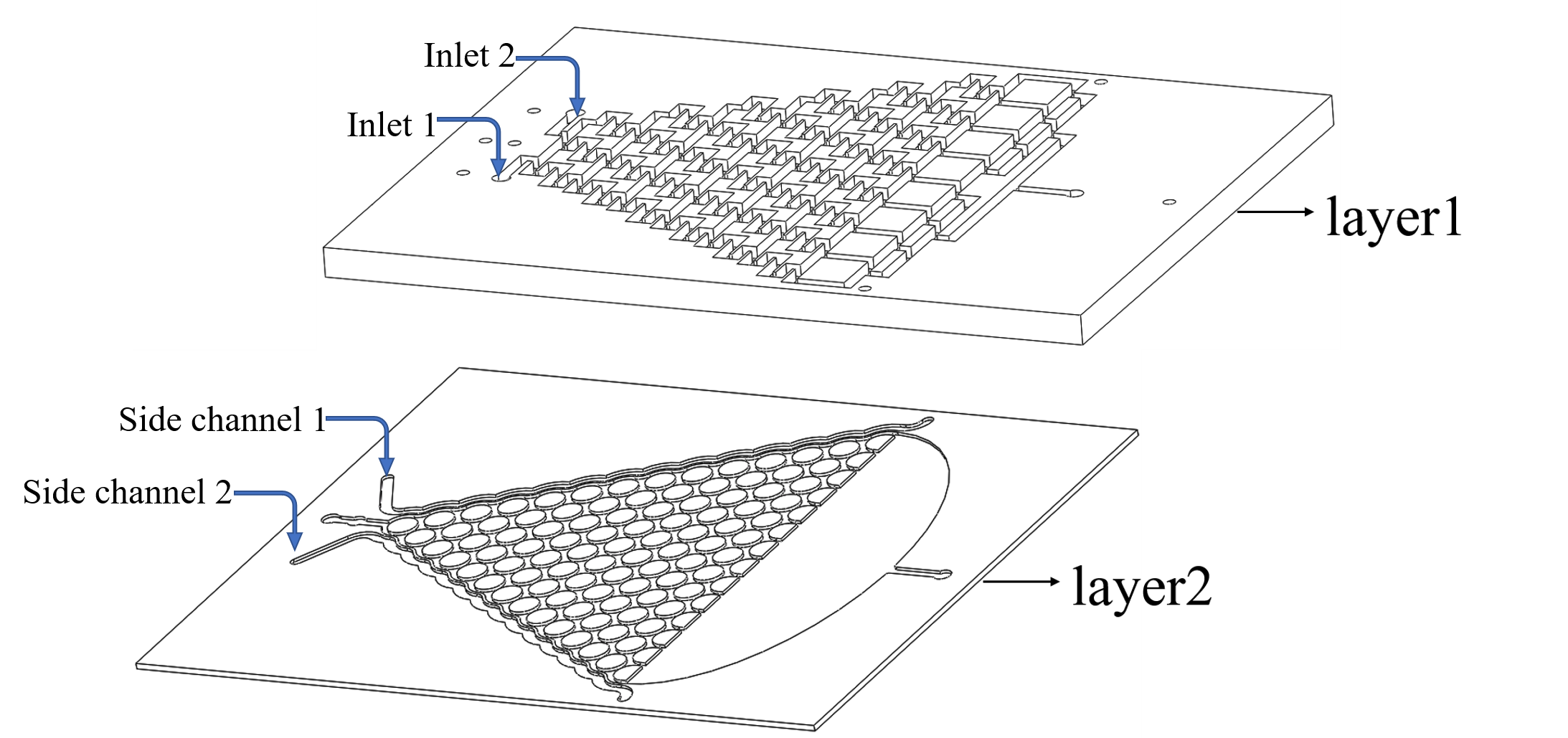
To warrant the success of the experiment, we have 2 plans to form a chemical concentration gradient in the microfluidic chip.
Plan A: Use layer1 to mix the chemicals from the inlets.
Plan B: Input the liquid to the side channel in layer2. (Fig.1)
In this model, we only concern the situation in Plan A because theoretically this method can lead to more stable concentration gradient than Plan B dose.
Considering the time consumption of the diffusion process, we need to determine the Delaying Time (the interval between the time of adding chemicals and the time that it forms desired concentration gradient in the bottom later and the worms can be added) in our experiment.
The Delaying Time is determined by two processes:
• We inject the certain chemical into the first layer to form a concentration gradient (Fig.2).
• Gas molecules diffuse downward across the PDMS layer and reach the second layer.
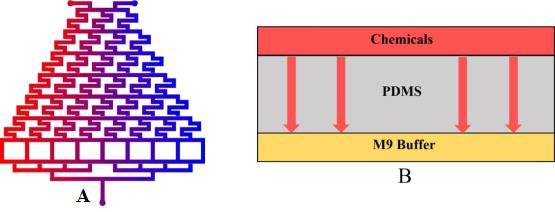
After that, the worms in the Layer2 can respond to the gradient chemical (diacetyl or 2-nonanone). We are able to determine whether their behavior is close to the wild types. See another model.
Physical Process
1. Forming Concentration Gradient
We need to know the time for forming the uniform concentration gradient. The characteristic diffusion time tc can be calculated by the Einstein and Brownian movement equation(Yang, Wu, Xu & Wang, 2011)[1]:
t=\frac{w^{2}}{2D}
Here, w is the diffusive distance, which is equal to half of the width of the branch channel (In our work, the width of any serpentine branch channel is 0.15 mm.);
D is the diffusion coefficient of the molecule in liquid.
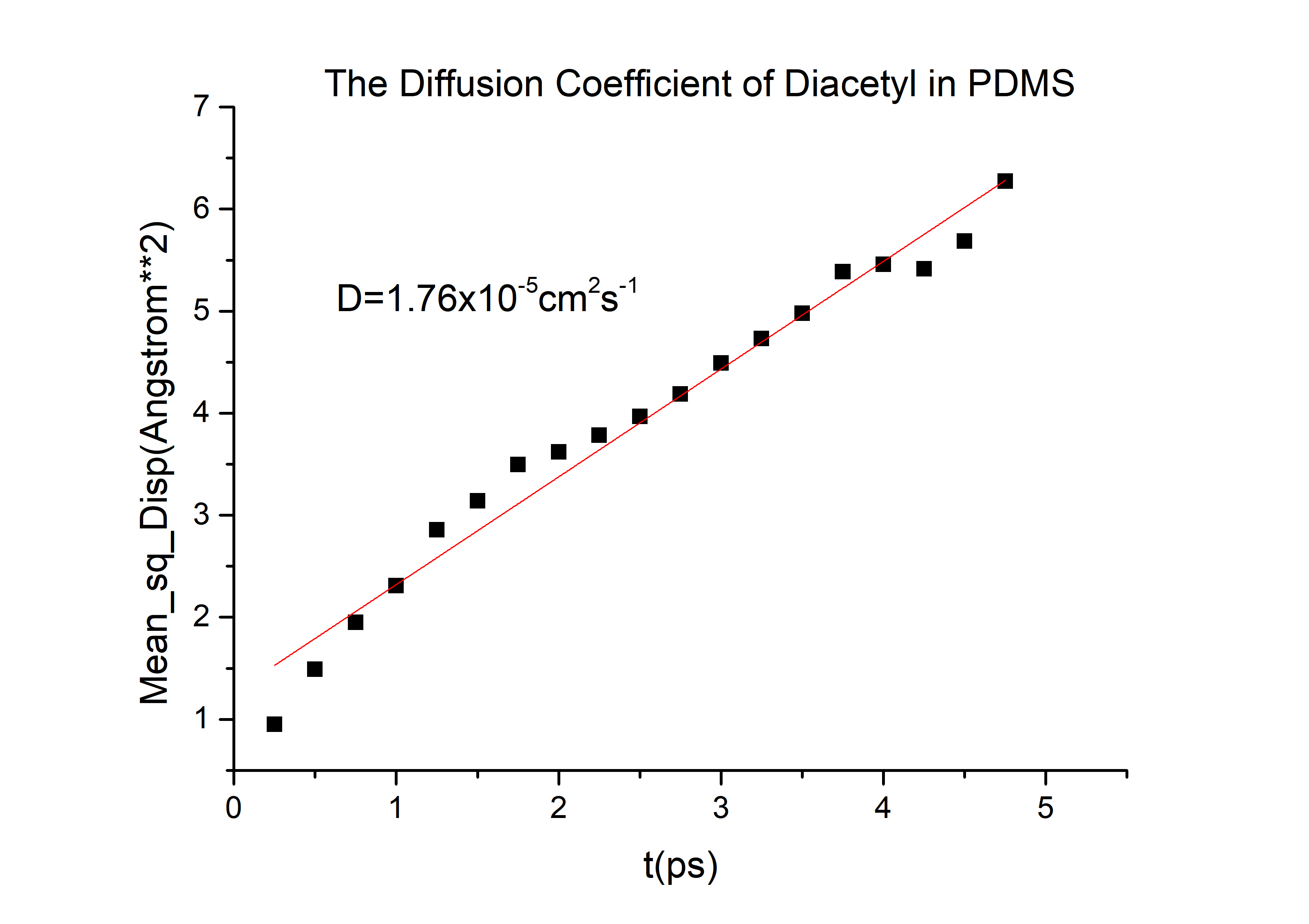
The D value of the diacetyl is 8.5*10-6cm2s-1
Based on the above formulas and parameters, we can get our tc=3.3s. It means that it costs 3.3s to form the expected gradient in layer1.
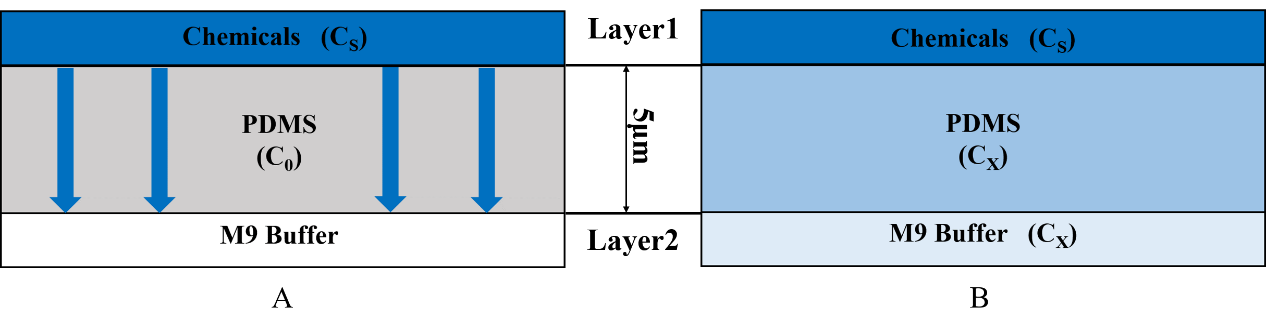
2.The Diffusion Time for Chemicals in PDMS
The process that gas molecules diffuse downward across the PDMS layer is considered. The second layer is full of the continual M9 buffer flow, so the chemicals will not be accumulated in this layer. We can assume that the concentration of layer2 is always equal to the concentration at the bottom of the PDMS.
A simplified diffusion model is built to describe the physical process:
For nonsteady-state diffusion, we use Fick’s second law to describe the process
\frac{C_x-C_0}{C_s-C_0}=1-erf(\frac{x}{2 \sqrt{Dt}})
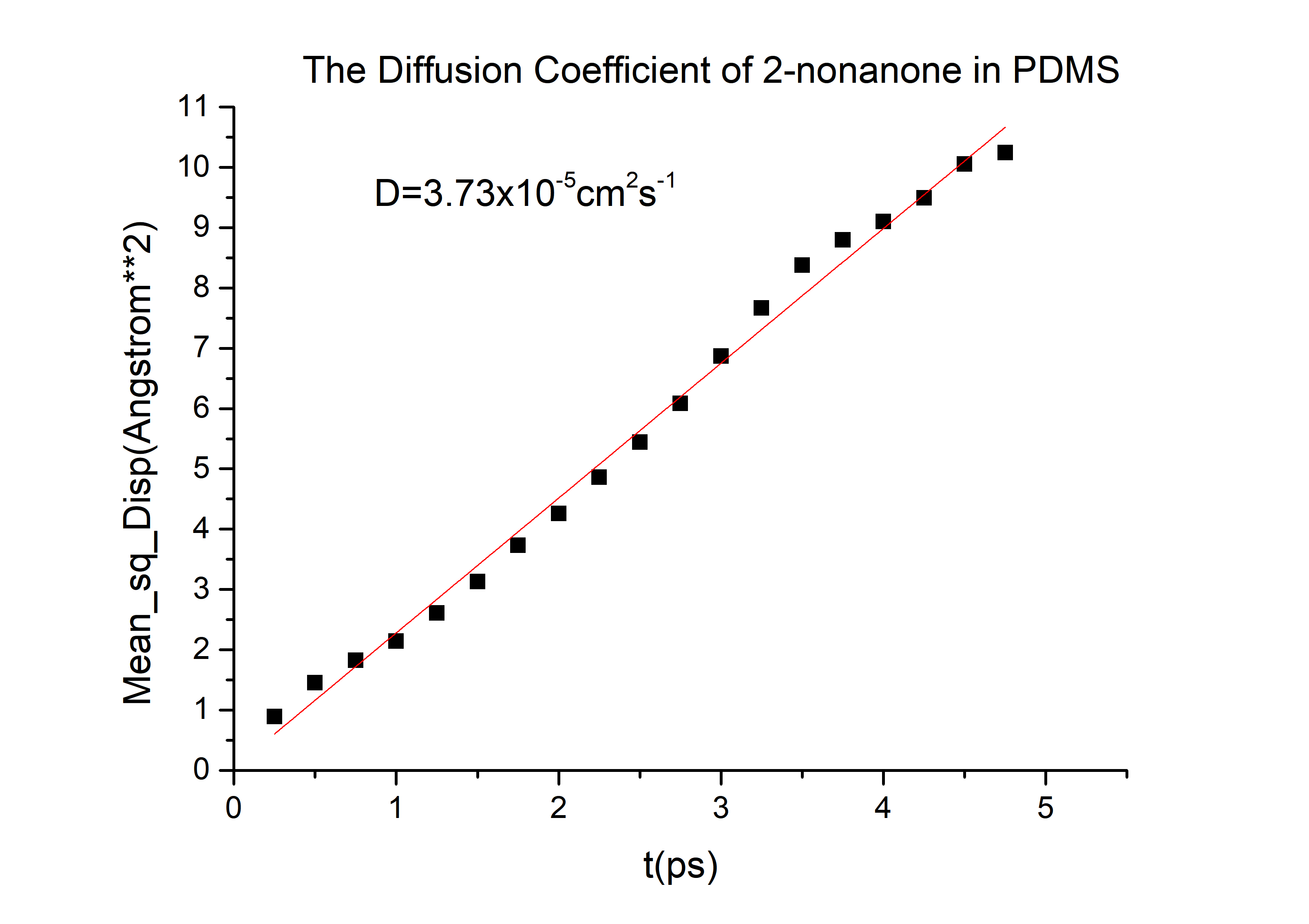
D(2-nonanone) = 6.78*10-6cm2/s in PDMS.
D(diacetyl) = 6.78*10-6cm2/s in PDMS.
Calculation details are shown in The Calculation of Diffusion Coefficient D
Concentration C is related to the position (distance x within PDMS) and the time variable t[2].
For t=0, C=C0 at 0≤x≤∞;
For t>0, C=Cs (the constant surface concentration) at x=0;
C=C0 at x=∞ And then there is a general solution: Where Cx represents the concentration at distance x after time t.
\frac{x}{2 \sqrt{Dt}}=constant, so if this constant can be calculated, the equation of distance x and time t can also be gotten.
In our model, C0=0, so the equation is changed to \frac{C_x}{C_s}=1-erf(\frac{x}{2 \sqrt{Dt}})
Cx represents the concentration at distance x that C. elegans can feel.
Cs is the initial concentration of the chemical gas.
We need to know the fractions of the chemicals in the gas because only the gas molecular can across the PDMS.
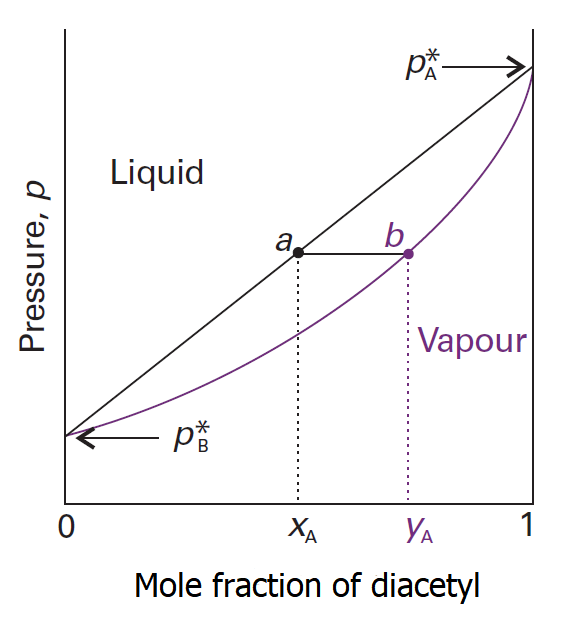
For ideal mixture of the two pure liquids, the compositions of the liquid and vapor follows from Dalton’s law that the mole fractions in the gas, yA (the mole fraction of diacetyl) and yB (the mole fraction of water) [3], are
y_A=\frac{p_A}{p}\qquad y_B=\frac{p_B}{p}
pA and pB are the partial vapor pressure of component A and component B in the mixture, they follow the Raoult’s law:
p_A= x_A\cdot p^*_A\qquad p_B= x_B\cdot p^*_B
where p*A is the vapour pressure of pure A and p*B is that of pure B. The total vapor pressure p of the mixture is therefore:
p= p_A+p_B =x_\cdot^*_A + x_\cdot^*_B= p^*_B+(p^*_B-p^*_A)
According to the Dalton’s law and the Raoult’s law we can get:[4]
y_A=\frac{x_A\cdot p^*_A}{p^*_B+(p^*_B-p^*_A)}
For diacetyl:
In Layer1, xA is the mole fraction of diacetyl in liquid mixture: the concentration in liquid Cliquid =100uM is the mole fraction in liquid xA =1.8*10-5, so the mole fraction in gas yA =5.4*10-5 is theconcentration in gas Cgas = 300uM
In Layer2, the xA is the mole fraction of diacetyl in liquid mixture: the concentration in liquid Cgas = 1uM (A suitable concentration of diacetyl which can be sensed by the worms [5]) is the mole fraction in liquid xA =1.8*10-7, so the mole fraction in gas yA =5.4*10-7 is the concentration in gas Cgas = 3uM .
According to the equation we can get that the erf(\frac{x}{2 \sqrt{Dt}})=1-\frac{C_x}{C_s}=0.99 and then referred to the Table 1 we can get that the \frac{x}{2 \sqrt{Dt}}=1.8.
t=0.1s
Conclusion
According to the two situations of the Delaying Time:
The time for complete diffusive mixing of diacetyl: tc = 3.3s.
The time for diacetyl diffusion through PDMS layer: td = 0.1s.
Compared to the time used to form the concentration gradient in Layer1, this time is negligible. Thus, about 3.4s after we add the chemicals, we can start to count the number of the worms about their response to chemicals.
For 2-nonanone, similarly, the total time cost is 3.1s.
It demonstrates that our microfluidic device is precisely controlled.
The Calculation of Diffusion Coefficient D
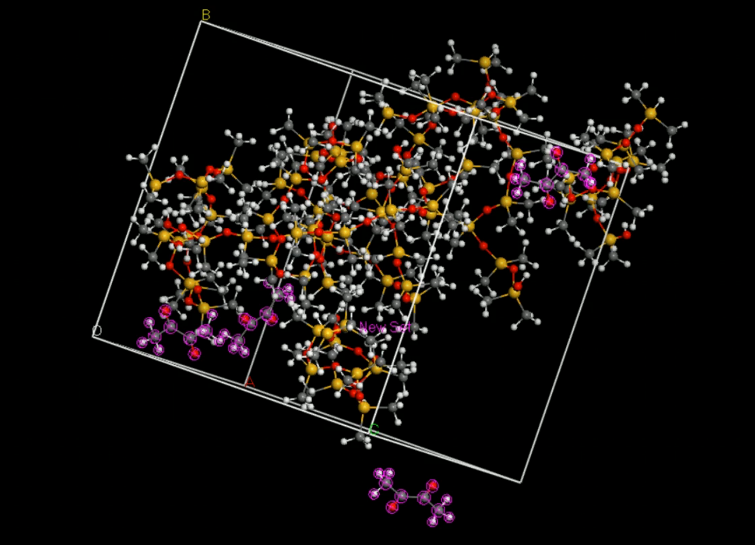
The diffusivity of a gas in an organic solvent, polymer, or zeolite can be calculated by simulating the molecular dynamics process and calculating the mean square displacement of the gas in the material. This allows us to calculate the self-diffusivity coefficient of the gas and gives an insight into the overall diffusivity. As we are performing a molecular dynamics calculation, we can analyze the effect of temperature, pressure, density, and penetrant size and structure on diffusion. We used force-field method to calculate the D in PDMS by Material Studio® (MS) a software for material calculation.[6][7]
Set up the initial structures
First, we set up the initial structure of the PDMS and the chemicals (Fig.5 and Fig.6).
Build an amorphous cell
Then, we put the two molecules in to an amorphous cell (Fig.8).
Relax the cell
When we generate an amorphous cell, the molecules may not be equally distributed throughout the cell, creating areas of vacuum. To correct this, we must perform a short energy minimization to optimize the cell. After the minimization, we should run a short molecular dynamics simulation to equilibrate the cell.
Run and analyze molecular dynamics
Export data and calculate the diffusivity
Then we can got the D of 2-nonanone and diacetyl:
D(2-nonanone) = 6.78*10-6cm2/s
D(diacetyl) = 6.78*10-6cm2/s
References
- ↑ Yang, C., Wu, Y., Xu, Z., & Wang, J. (2011). A radial microfluidic concentration gradient generator with high-density channels for cell apoptosis assay. Lab On A Chip, 11(19), 3305. http://dx.doi.org/10.1039/c1lc20123a
- ↑ Callister, W. D., & Rethwisch, D. G. (2004). Fundamentals of Materials Science and Engineering. John Wiley and Sons Ltd.
- ↑ Hofmann, D., Fritz, L., Ulbrich, J., Schepers, C., & Böhning, M. (2000). Detailed‐atomistic molecular modeling of small molecule diffusion and solution processes in polymeric membrane materials. Macromolecular Theory & Simulations, 9(6), 293–327.
- ↑ S. G. Charati† and, & Stern, S. A. (1998). Diffusion of gases in silicone
- ↑ Albrecht, D. R. and C. I. Bargmann (2011). “High-content behavioral analysis of Caenorhabditis elegans in precise spatiotemporal chemical environments.” Nature Methods 8(7): 599-605.
- ↑ S. G. Charati† and, & Stern, S. A. (1998). Diffusion of gases in silicone polymers: molecular dynamics simulations. Macromolecules, 31(16), 5529-5535.
- ↑ Hofmann, D., Fritz, L., Ulbrich, J., Schepers, C., & Böhning, M. (2000). Detailed‐atomistic molecular modeling of small molecule diffusion and solution processes in polymeric membrane materials. Macromolecular Theory & Simulations, 9(6), 293–327.