Team:SUSTech Shenzhen/Model1

Chemical Diffusion

Model

This model is built to simulate the diffusion process of chemicals in the PDMS chips, and through that we are able to determine the “delaying time” of the C. elegans’ olfactory response in our inducing experiment.

The experiment is designed to demonstrate that the insertion does not damage the olfactory receptor neuron pair by testing their response to diacetyl and 2-nonanone. We assume that if the neuron pairs is unaffected, the modified worms will respond to the chemicals as the wild types do. We have 2 methods to form a concentration gradient in the microfluidic chip.

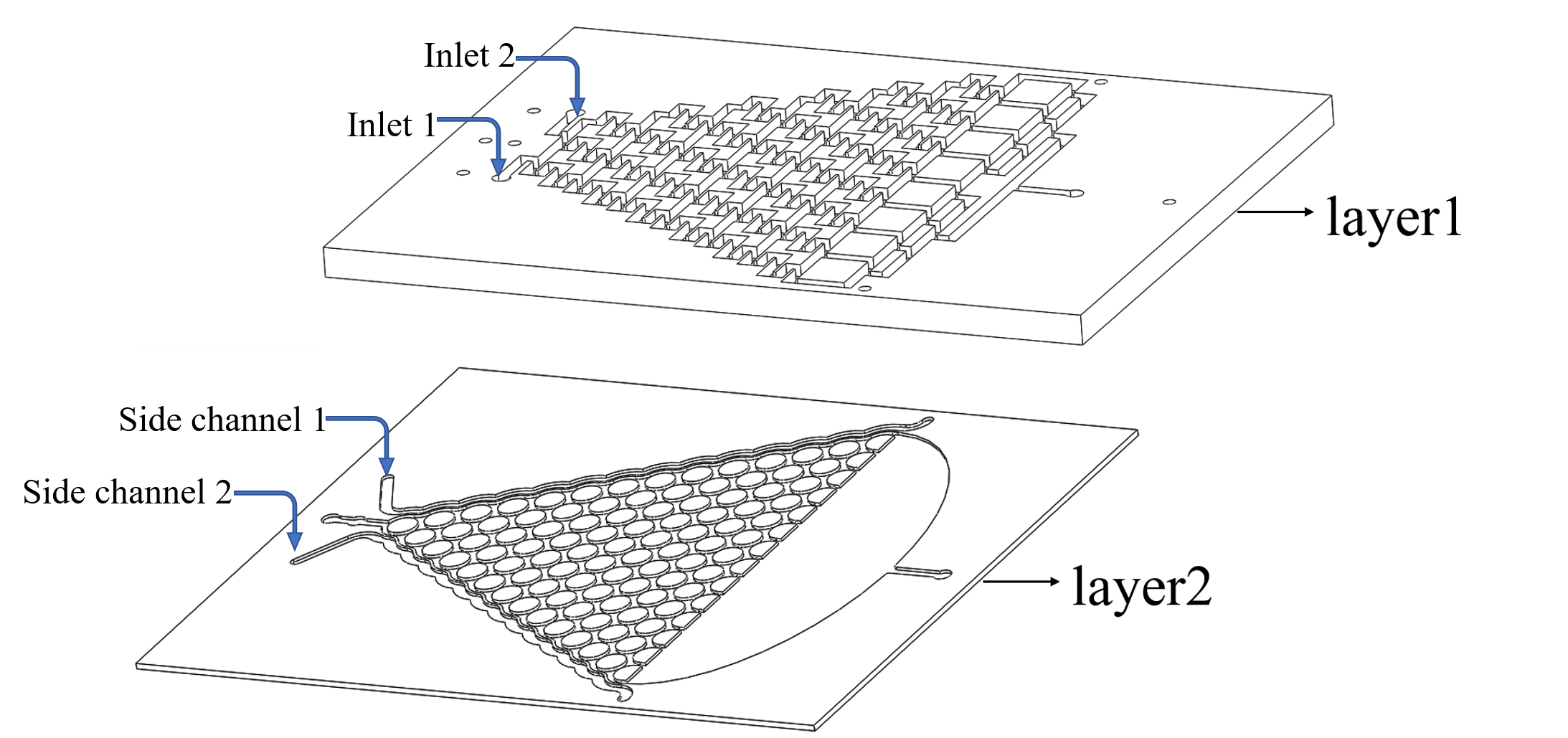
• Use layer1 to mix the chemicals from the inlets.

• Input the liquid to the side channel in layer2.

In this model, we only concern the situation in first method, the process that the gas molecules in layer1 will permeate through PDMS layer to layer2 (the chamber holding the worms).

Fig.1 The microfluidic chip We inject the chemicals in chemicals inlet2 and water in inlet1 in layer1 to form the concentration gradient or we can inject the chemicals in side channel1 and water in side channel2 to form the concentration difference in layer2

This plate consists of two layers. We inject the chemicals into the first layer to form a concentration gradient. Gas molecules diffuse downward across the PDMS layer and reach the second layer. Then the worms in the second layer can respond to the chemicals(diacetyl and 2-nonanone).

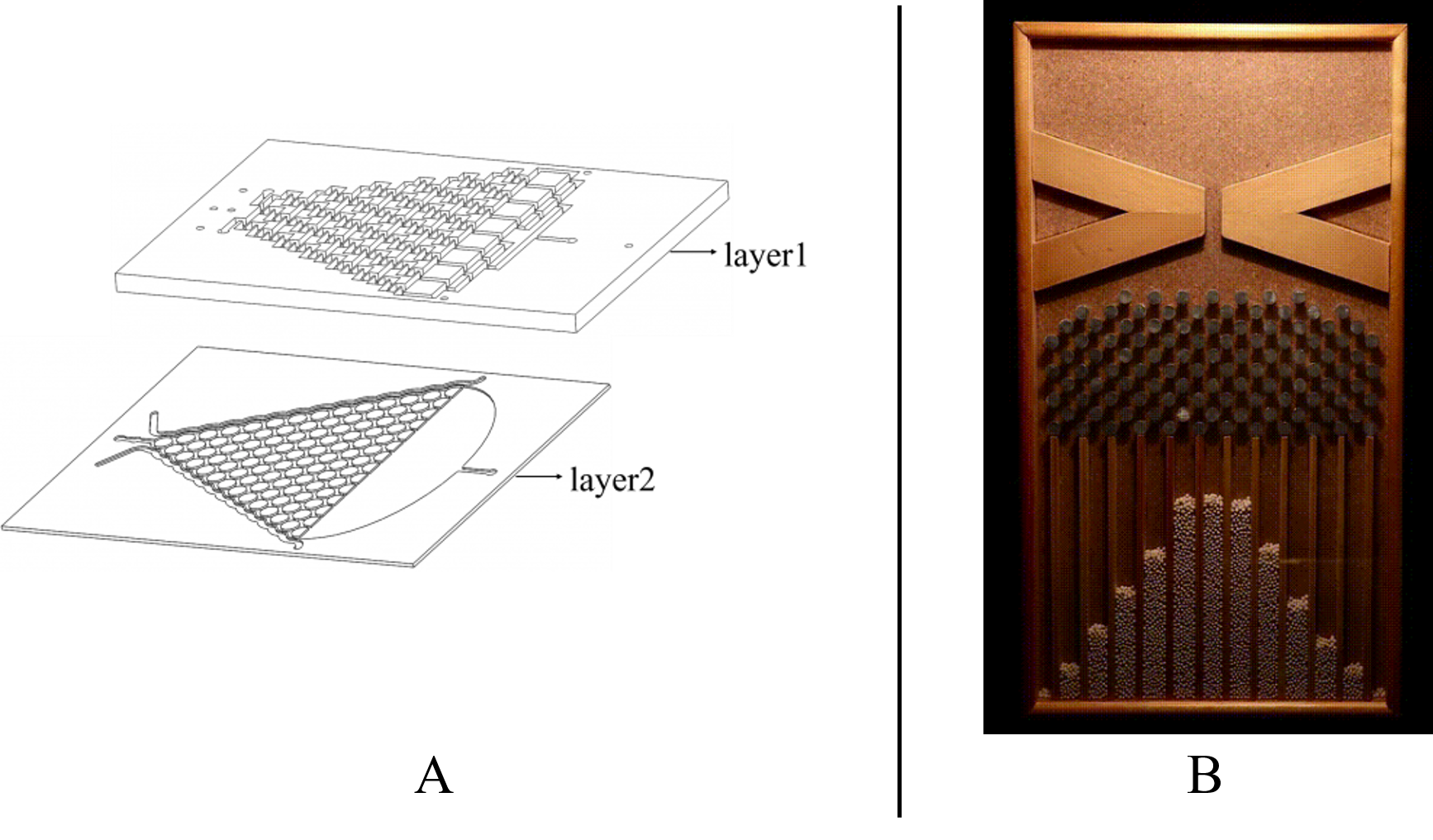
The chamber in layer2 is just like the Galton Nail Plate. We designed call it the Gaussian Plate in our project (Fig.1 the Gaussian Plate)

Fig.2 The Gaussian plate Using this chip, we can know the C. elegans’ preference and repulsion through their distribution in the chip.

One important thing is to know how long the diffusion process will cost from the layer1 to layer2, and we are able to know the “delaying time” of the response of the worms to the chemicals. (Fig.3).

Fig.3 A) The chemicals diffuse downward across the PDMS. B) The chemical can across the PDMS to enter in the M9 buffer (KH2PO4 3 g, Na2HPO4 6 g, NaCl 5 g, MgSO4 (1M) 1 ml dH2O 1 L). The M9 buffer is injected into the layer2 continually so the chemicals will not be accumulated in the M9 buffer, on the other words the concentration of layer2 is always equal to the concentration at the bottom of the PDMS.

Physical Process

For nonsteady-state diffusion, there is an equation named Fick’s second law: \frac{\partial C}{\partial t}=D \frac{\partial^2 C}{\partial x^2}

The constant of proportionality D is called the diffusion coefficient, which is expressed in square meters per second. Concentration C is plotted versus position (or distance) within the solid x and the time t.

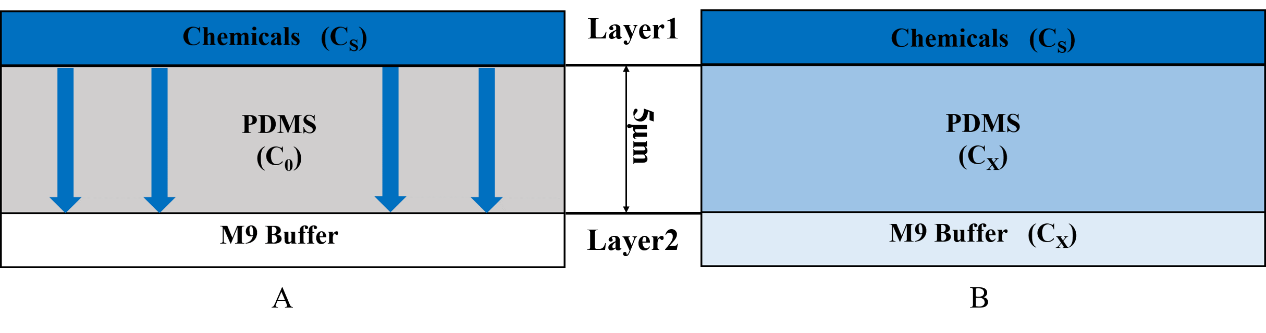
For t=0, C=C₀ at 0≤x≤∞;

For t>0, C=C_s (the constant surface concentration) at x=0;

C=C₀ at x=∞. And then there is a general solution: \frac{C_x-C_0}{C_s-C_0}=1-erf(\frac{x}{2 \sqrt{Dt}}) Where C_x represents the concentration at distance x after time t.

\frac{x}{2 \sqrt{Dt}}=constant, so if this constant can be calculated, the equation of distance x and time t can also be gotten.

In our model, C₀=0, so the equation is changed to \frac{C_x}{C_s}=1-erf(\frac{x}{2 \sqrt{Dt}}) C_x represents the concentration at distance x that C. elegans can feel. C_s is the concentration set by our own and it is a constant. x is 5mm (Fig.4).

Fig.4 The diffusion in the Gassian chip We set that the C_x = 1uM (for diacetyl) ,the optimum concentration can be sensed by the C. elegans. We set that the C_s = 288uM (for diacetyl),

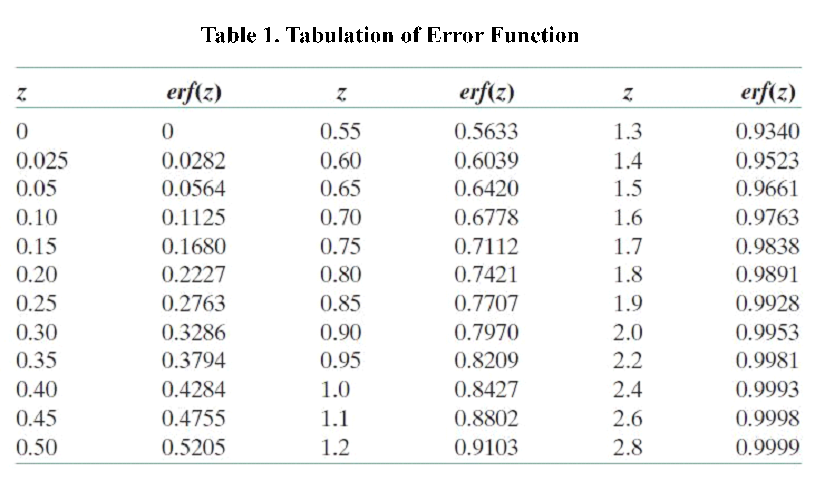
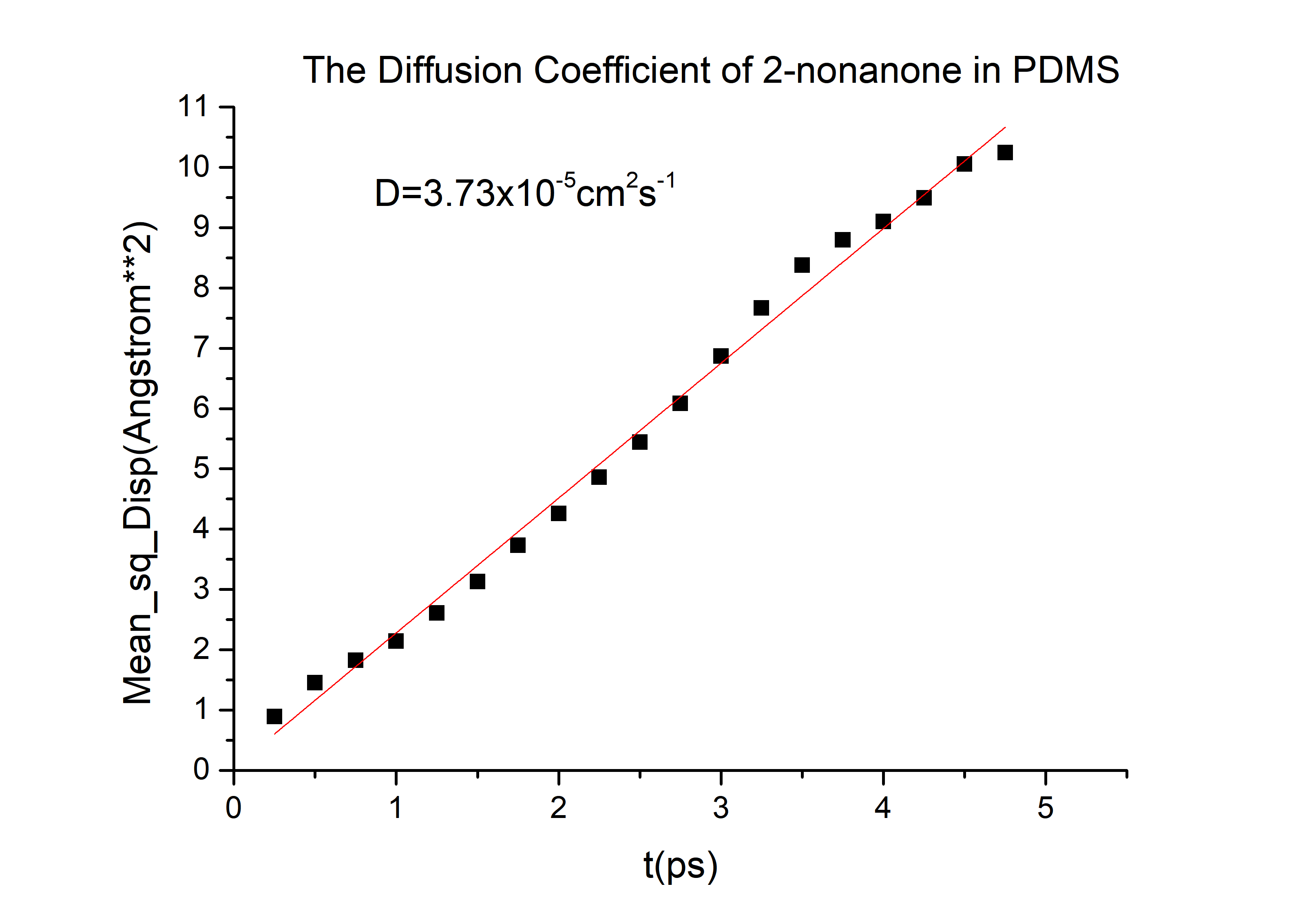
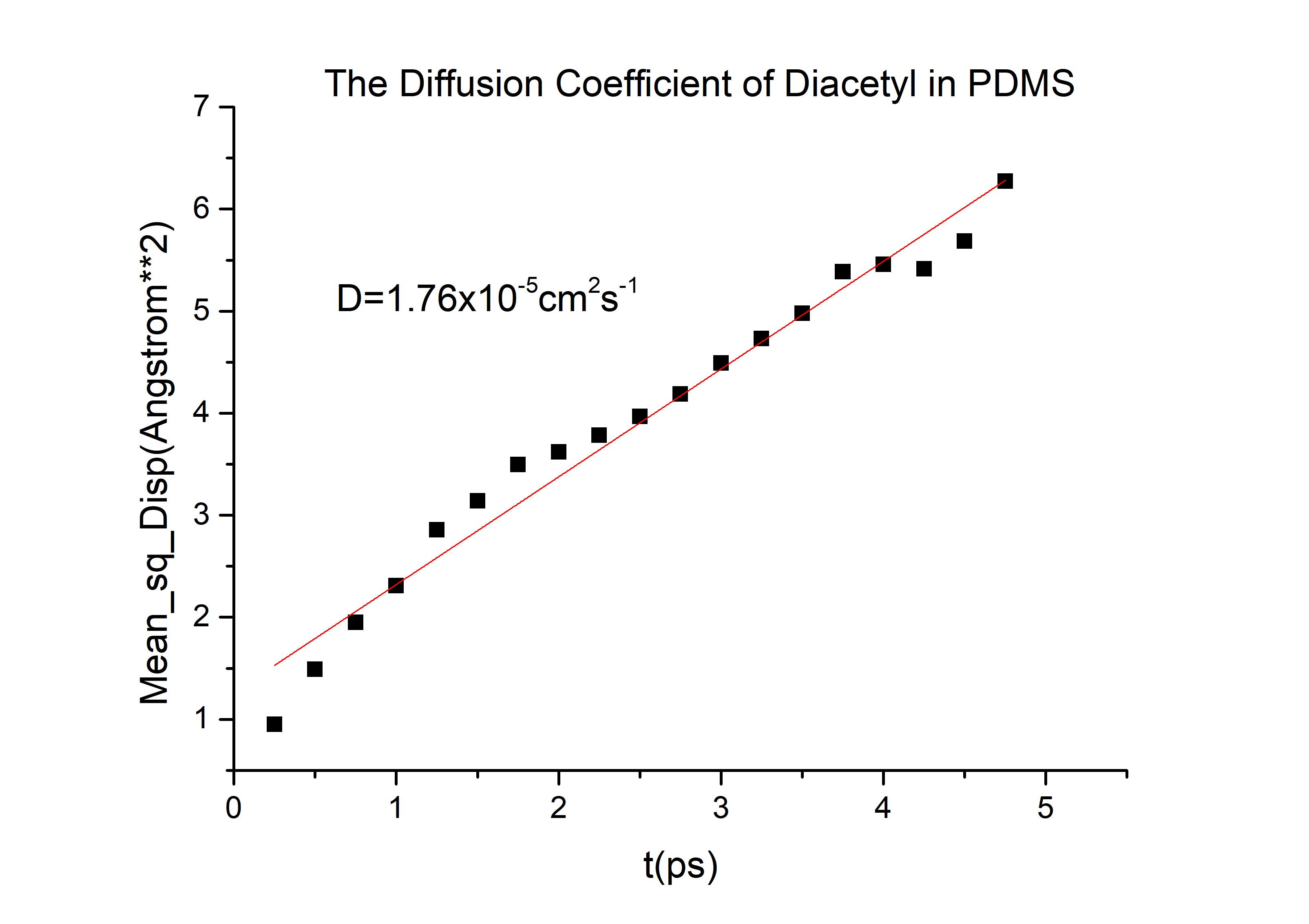
According to the equation we can get that the erf (\frac{x}{2 \sqrt{Dt}})=0.9965 and then referred to the Table 1.1 we can get that the \frac{x}{2 \sqrt{Dt}}=2.2, and D is the diffusion coefficient for 2-nonanone or diacetyl in PDMS. We need to calculate the D to get the time t according to the equation. We used the force-field method to get the D of those two chemicals (the concrete operational process is shown in 1.3).

D_(2-nonanone) = 6.78*10^-6cm²/s

D_(diacetyl) = 6.78*10^-6cm²/s

Finally, we can get the time t = 12 mins, on the other words, we cannot inject the C. elegans until the chemicals are injecting for 12 mins in layer 1(for diacetyl).

The Calculation of Diffusion Coefficient D

The diffusivity of a gas in an organic solvent, polymer, or zeolite can be calculated by simulating the molecular dynamics process and calculating the mean square displacement of the gas in the material. This allows us to calculate the self-diffusivity coefficient of the gas and gives an insight into the overall diffusivity. As we are performing a molecular dynamics calculation, we can analyze the effect of temperature, pressure, density, and penetrant size and structure on diffusion. We used force-field method to calculate the D in PDMS by Material Studio_® (MS) a software for material calculation.

Set up the initial structures

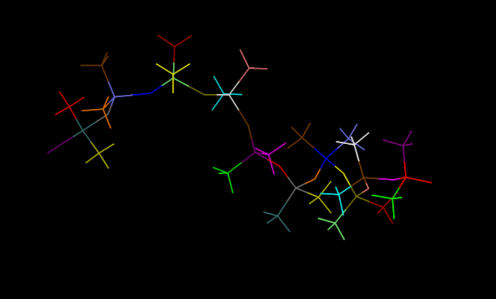
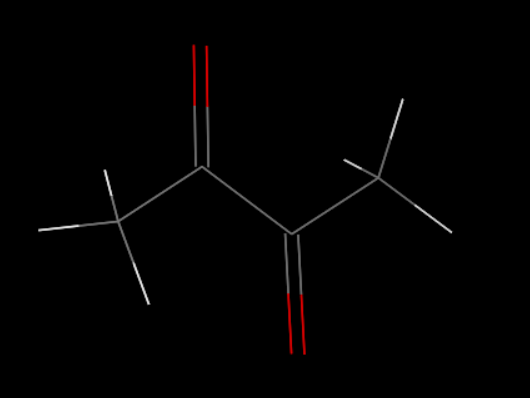
First, we set up the initial structure of the PDMS and the chemicals (Fig.5 and Fig.6).

Fig.5 The structure of PDMS

Fig.6 The structure of diacetyl

Build an amorphous cell

Then, we put the two molecules in to an amorphous cell (Fig.7).

Fig.7 The amorphous cell

Relax the cell

When we generate an amorphous cell, the molecules may not be equally distributed throughout the cell, creating areas of vacuum. To correct this, we must perform a short energy minimization to optimize the cell. After the minimization, we should run a short molecular dynamics simulation to equilibrate the cell.

Fig.8 The cell after relaxing

Run and analyze molecular dynamics

Export data and calculate the diffusivity

Then we can got the D of 2-nonanone and diacetyl:

D_(2-nonanone) = 6.78*10^-6cm²/s

D_(diacetyl) = 6.78*10^-6cm²/s

Fig.9 The diffusion coefficient of 2-nonanone in PDMS

Fig.10 The diffusion coefficient of diacetyl in PDMS

References

Made by from the elegans.Inc in SUSTech_Shenzhen.

Licensed under CC BY 4.0.

• ©2017 SUSTech_Shenzhen