Genetic Probability
Model
Contents
Genetic probability model
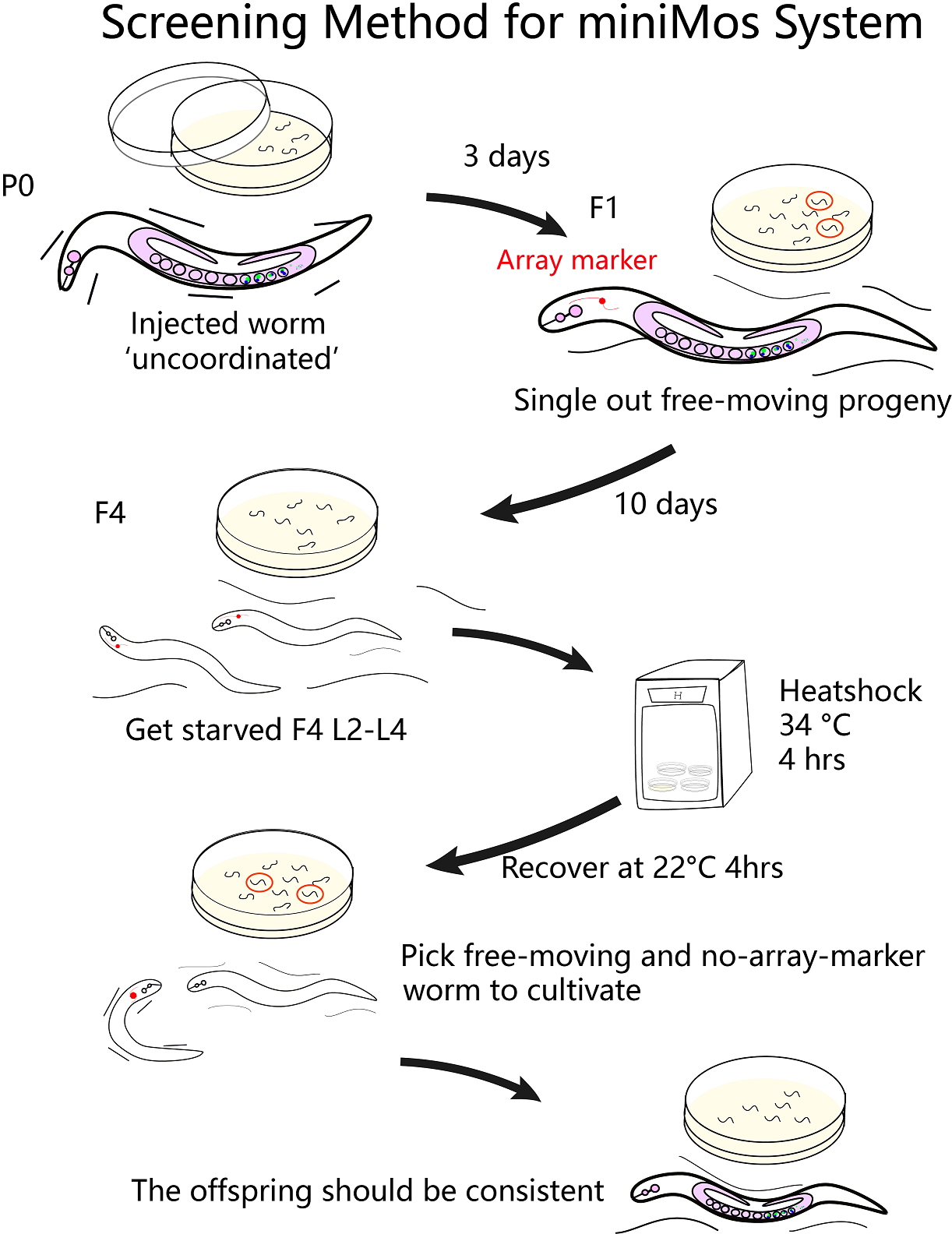
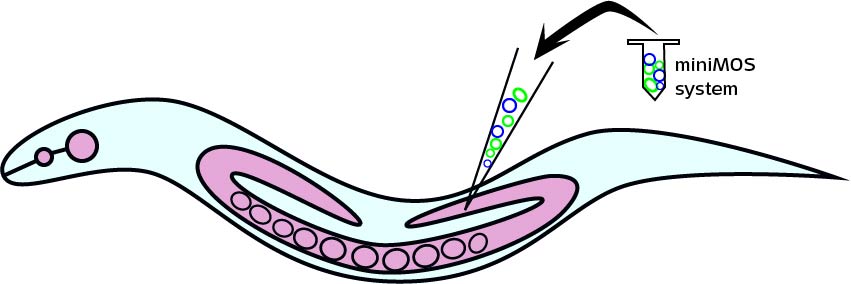
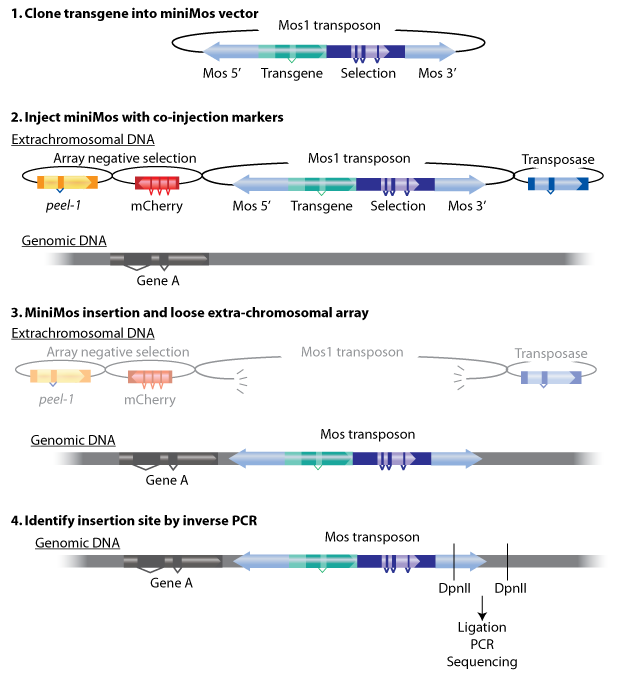
In our project, we aim to get C. elegans strains with the preference for blue lights and the aversion for red lights by miniMos injection. Therefore, we build a miniMos injection model in order to simulate and estimate numbers of injected worms that can expressed two phenotypes.
The successful rate of miniMos injection
First we need to consider the successful rate of miniMos system. The microinjection needs accurate operations to inject plasmids into C. elegans gonads, which allows plasmids to enter the embryos and maintain the phenotypes. Therefore, accurate manual operations can lead to a promising result. According to the miniMos protocol, the probability of correct injection is approximately 60% excluding manual errors, and about 10% of F1 can be rescued, meaning that the plasmid expression rate(transposon transfers target gene into chromosomes) is about 10%.[1] So the successful rate is:
accurate rate of manual operation * plasmid expression rate = 60% * 10% = 6%.
The stable inheritance rate
After got heterozygote F1 via miniMos injection, our next step is to get stable expression worms in F2 generation. During the F2 generation, based on the Mendel's laws, if two genes are located on different chromosomes, their alleles will segregate independently during the formation of gametes. And Mendel calculated the probability of getting stable expression F2, the ideal rate is \frac{1}{16}. Therefore, in our experiment, the prospecting result of getting target strains is also \frac{1}{16}.
The ideal result
Therefore, the overall probability of getting the target strain is: (accurate rate of manual operation ) * (plasmid expression rate) * ( F2 stable expression rate ) * 100% = 60% * 10% * \frac{1}{16}*100% = 0.004.
The effect of crossing over
However, this probability does not consider the chance of crossing over. Crossing over is the exchange of genetic materials between homologous chromosomes and results in recombinant chromosomes during sexual reproduction.[2] Therefore, crossing over may affect the rate of stable inheritance by exchanging genetic materials. According to the formula, the rate of crossing over is: (numbers of recombinant genotype offspring)/(numbers of total offspring)*100%
Therefore, the possible rate of crossing over in our experiment is: \frac{10}{354}=\frac{5}{177}
And the final rate is : 0.004*(1-\frac{5}{177})=\frac{86}{22125}=0.3%
\0.004\times ( 1-frac{5}{177} )=\frac{86}{22125}=0.3 \times
The fitness of our model with our real data
Based on our model, we calculate the probability of getting the genetic stable worms in order to precisely implement our experiments. More importantly, our modeling reliability has been tested and confirmed by comparing the calculated result with raw results from the experiments. 1) The rate of miniMos injection is about 6%, that is six worms with correct insertions within 100 worms. And in reality, we actually obey this probability. In our project, we injected about 500 worms in total, and finally got about 25 worms with expected insertions. 2) The probability of getting stable inheritance F2 is \frac{1}{16} in theory, and we found 2 plates of worms showed both GFP and RFP at the site of neurons among 40 F2. Overall, these results showed that our model is a good guidance to explain our results, it is feasible.
References
- ↑ http://www.wormbuilder.org/minimos/commentsfaq/
- ↑ Griffiths, AJF; Gelbart, WM; Miller, JH; et al. (1999). "Modern Genetic Analysis: Mitotic Crossing-Over". New York: W. H. Freeman.