Joe McKeown (Talk | contribs) |
Joe McKeown (Talk | contribs) |
||
| Line 59: | Line 59: | ||
<center> | <center> | ||
<div class="row"> | <div class="row"> | ||
| + | <div class="col-md-1"></div> | ||
<div class="col-md-4"> | <div class="col-md-4"> | ||
<img src="//2017.igem.org/wiki/images/1/15/IGEM-York-Individual-Frame.png" style="border-style: solid; border-color: #000; border-radius: 25px; border-width: 3px;" width="100%"></li> | <img src="//2017.igem.org/wiki/images/1/15/IGEM-York-Individual-Frame.png" style="border-style: solid; border-color: #000; border-radius: 25px; border-width: 3px;" width="100%"></li> | ||
| Line 68: | Line 69: | ||
<p style="font-size: 18px; text-align: center;">A representation of a stack of refocused images.</p> | <p style="font-size: 18px; text-align: center;">A representation of a stack of refocused images.</p> | ||
</div> | </div> | ||
| + | <div class="col-md-1"></div> | ||
</div> | </div> | ||
</center> | </center> | ||
Revision as of 04:28, 30 October 2017
Digital Inline Holographic Microscopy
How does it work?
Digital holographic microscopy makes use of diffraction. This a physical phenomenon wherein objects (or apertures) in the path of a source of waves will create patterns in the waves. These patterns depend on the shape of the objects themselves. Since electromagnetic waves are, somewhat unsurprisingly, waves, it is possible to use the diffraction of light to create patterns that we can see.
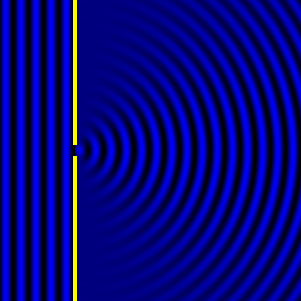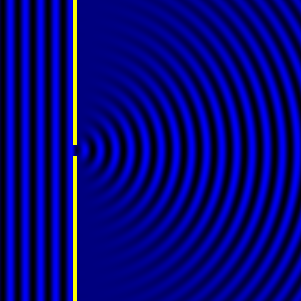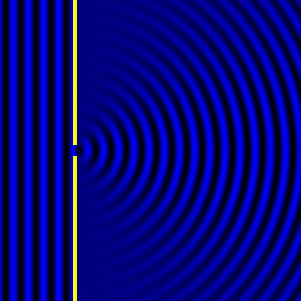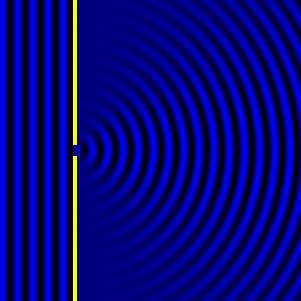
- Diffraction pattern caused by a slit of width equivalent to one wavelength [1].
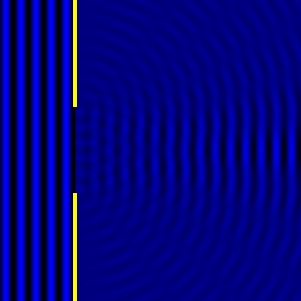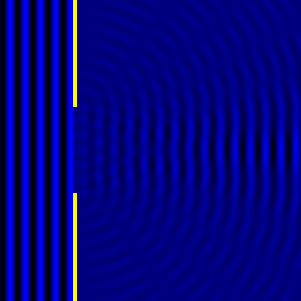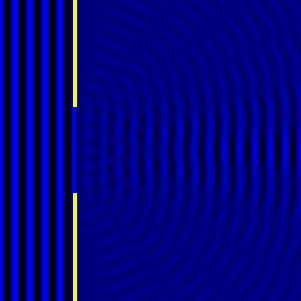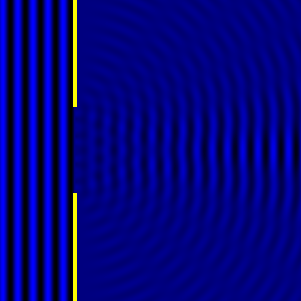
- Diffraction pattern caused by a slit of width equivalent to six wavelengths [1].
The above images show examples of patterns being formed in wavefronts by apertures in the path of otherwise uninterrupted waves. As can be seen by contrasting these images, the pattern created by a larger aperture is distinguishable from a smaller aperture's pattern. The particular distinctions can be described through mathematical formalisms. In particular, the shape of a diffraction pattern is the Fourier transform of the aperture that caused it. Likewise, the inverse Fourier transform of the diffraction pattern describes the aperture. Thence, once the diffraction patterns have been created, it is possible to infer the shape and size of the objects that caused them, if we also know the wavelength of the light source and the distance from the sample at which the patterns were observed.
Digital Holograms
When we perform Digital Inline Holography, we use the wavelength of light, an initial diffraction pattern, information about the size of each pixel and the aforementioned inverse Fourier transform to work out what the aperture (the sample) looked like. From this, we can construct an image showing what the diffraction pattern would look like at any distance. We perform this calculation many time to construct a stack of images, each of which represents a cross-section of the 3D space in the sample. When we put them all together, we have a hologram representing the entire sample.

An example of an initial diffraction pattern, from which a hologram can be created.

A representation of a stack of refocused images.
References
- [1]: Diffraction Formalism, Wikipedia, as on 4th September 2017 at http://en.wikipedia.org/wiki/Diffraction_formalism



