Overview
Model
Contents
Modeling is usually used to make sense of the experimental discovery in traditional biological studies. In this synthetic biology project, we believe that carefully carried out modeling will be critical for the experimental design and data analysis at different stages of the project. We hope to demonstrate that the modeling is especially helpful to finalize the microfluidics chip design, and determine the distribution of the C. elegans (Caenorhabditis elegans) in microfliudics, as well as the transfection of the MiniMos in our experiment.
Model for Chemical Diffusion
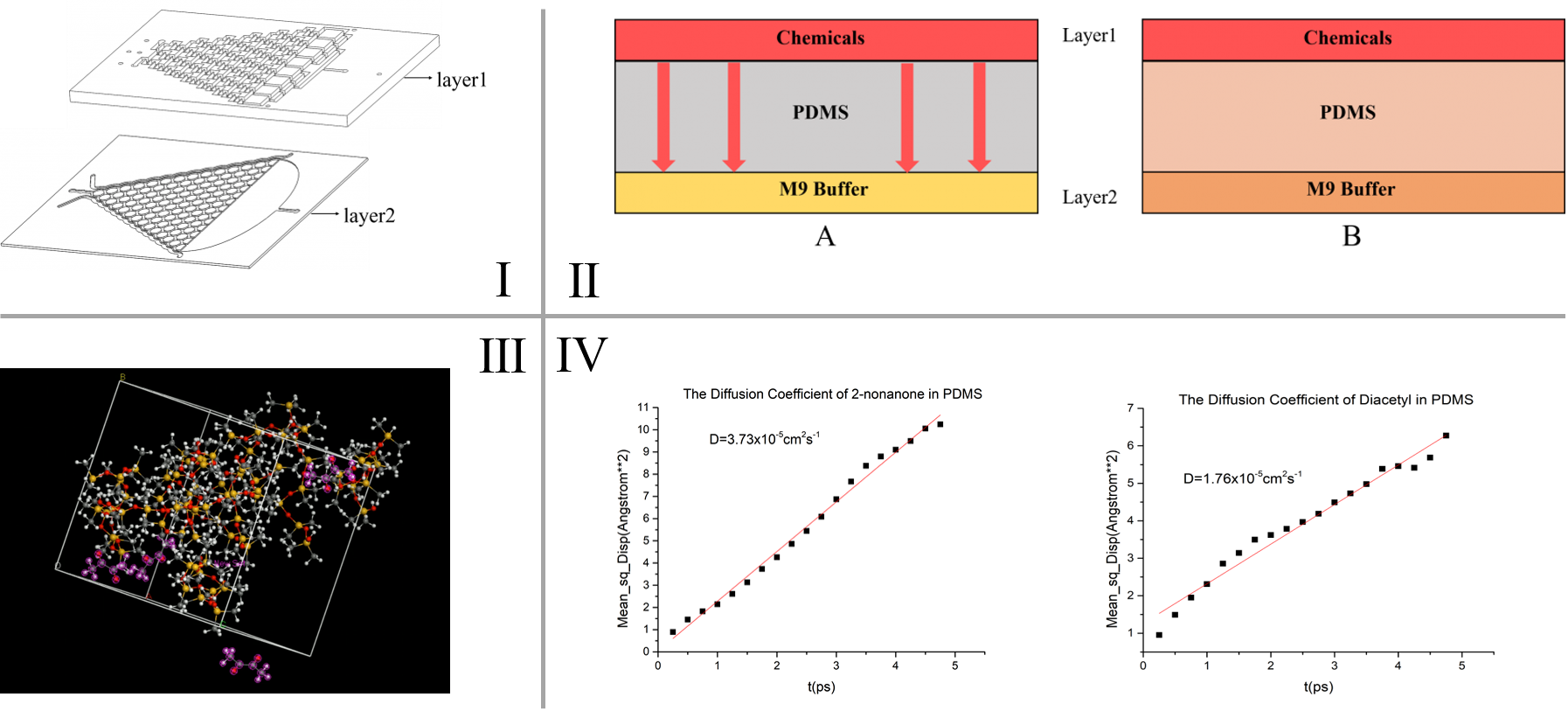
The diffusion process of chemicals in the PDMS chips is simulated in our model. 2 steps are included:
• The process to form a linear concentration gradient
• The chemical diffusion through the PDMS (Polydimethylsiloxane) layer
Total time consumption of the 2 processes is calculated, based on the Einstein and Brownian movement equation t=\frac{w^{2}}{2D} and Fick’s second law (\frac{\partial C}{\partial t}=D \frac{\partial^2 C}{\partial x^2}). The calculation results are used to guide our experiment design.
Model for Worms Locomotion
This model describes the locomotion of worms in the Gaussian Plate. It is applied in the experiment to demonstrate whether the genetic insertions undermine the functions of AWA and AWB neurons. If the neurons are not affected, worms will be attracted by diacetyl and repelled by 2-nonanone. Without adding these odorants, the distribution of the number of worms counted at each exit is close to the Normal distribution.
Parameter ka is introduced in the model considering the influence of the previous choice of C. elegans on the following one, and parameter kb represents the extent of their preference to certain chemicals.
Comparing the experiment statistics with the simulation result, we come to two conclusions:
- It is feasible to simulate the choice-making process of C.elegans in the Gaussian Plate.
- The turning side of the first step increase the possibility of choosing the same side at the next step by 30%.
Model for Neuron Network
The purpose of this model is to select promoters used in downstream neurons of C. elegans’ which have greatest possibility to be lighted on when AWA and AWB (the main neurons in our project) are actived.
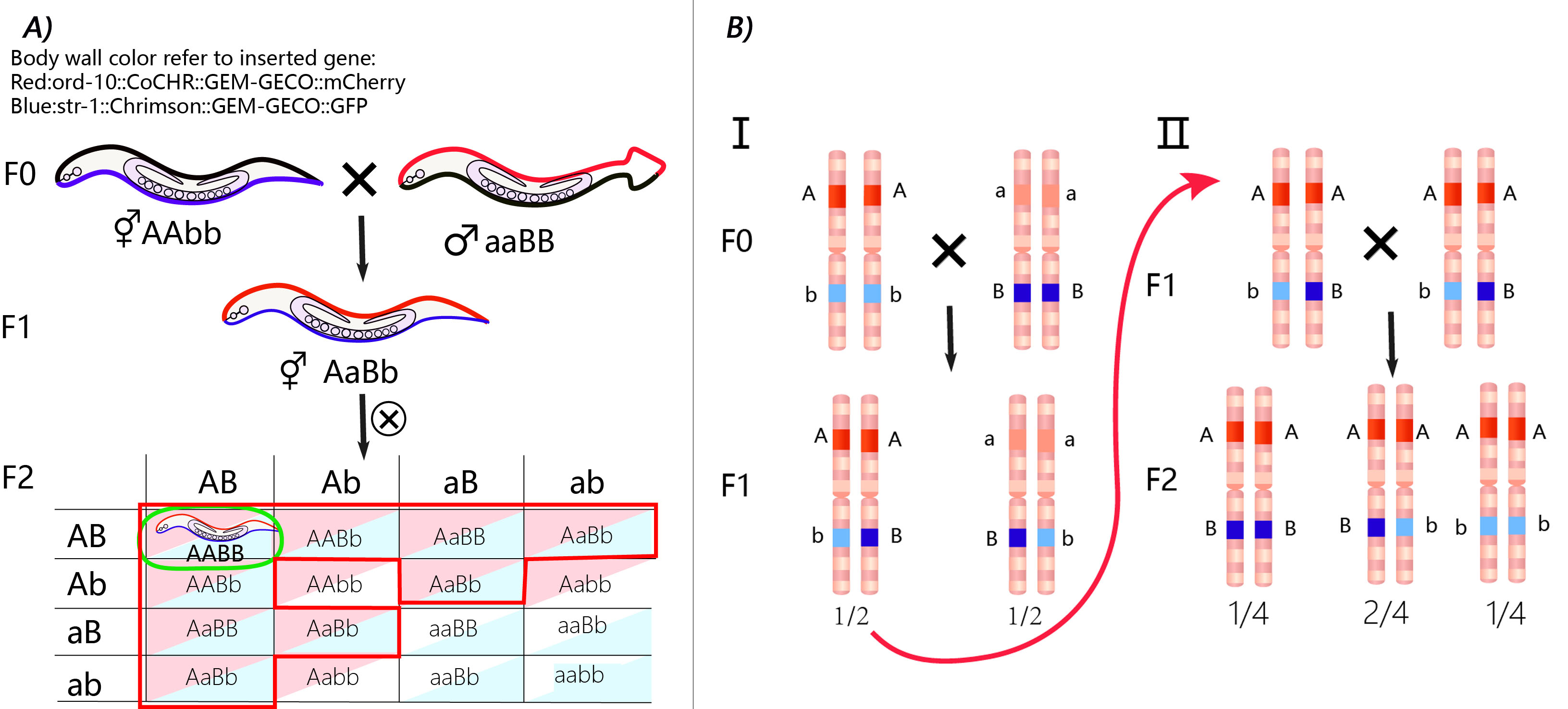
Model for Genetic Probability
This model describes the process in which we get 2 worm strains with stable genetic traits and the hybrid offspring. It was proposed at the beginning of our project to optimize our experimental design concerning how many worms we need to inject and how long it will take to make sure we get the expected result before iGEM Jamboree.
These 3 steps are considered in the model:
Inject plasmid (odr-10::CoCHR::GEM-GECO::mCherry and str-1::Chrimson::GEM-GECO::GFP) through miniMOS system.
Select the rescued worms using mCherry and GFP.
Mate the 2 strains to get the hybrid offspring of red fluorescence on AWA neuron and green fluorescence on AWB neuron.
Comparing the calculation and the experiment results, we demonstrate that the 2 strains that we finally get have the insertion gene on different chromosomes.